Ano ang mga digital na lagda at paano ito gumagana?

Ang mga pirma ng digital ay uri ng tulad ng mga elektronikong bersyon ng iyong mga pirma sa sulat-kamay. Pinapayagan nilang suriin ang mga tao pagiging tunay at integridad ng data, pati na rin ang pag-iwas sa signatory na hindi maitanggi (tanggihan) ang kanilang pagkakasangkot.

Ang mga pag-aari na ito ay humantong sa pag-ampon ng mga digital na lagda sa isang malawak na hanay ng mga aplikasyon, kabilang ang marami sa aming mga protocol ng seguridad, ligtas na email, at sa pamamahala ng mga digital na karapatan.

Sa artikulong ito, tatalakayin natin kung ano ang mga digital na lagda, kung saan ginagamit ang mga ito, pati na rin ang mga teknikal na detalye ng dalawa sa mga pinakasikat na algorithm, RSA at DSA.

Ano ang mga digital na lagda?

Tulad ng nakasaad sa itaas, ang mga pirma ng digital ay nagbibigay sa amin ng tatlong napakahalagang katangian. Ang mga ito ay pagpapatunay, integridad at hindi pagtanggi.

Pagpapatunay ay ang proseso ng pagpapatunay na ang indibidwal na nagpapadala ng isang mensahe ay tunay na sinasabi nila na sila, at hindi isang impostor.

Ang integridad ng data o isang mensahe ay tumutukoy kung ito ay nakarating sa parehong estado tulad ng noong ipinadala ito. Kung ang isang mensahe ay binago o pinalit, hindi na nito pinapanatili ang integridad nito.

Kung ang data o isang mensahe ay hindi maitatwa, nangangahulugan ito na hindi maaaring pagtatalo ng may-akda na sila ang tunay na tagalikha ng dokumento. Ang ari-arian na ito ay nag-aalis ng hindi maaaring mangyari, o ang dating “Paumanhin, ang aking kaibigan ay gumagamit ng aking account” na dahilan.

Hangga’t ang pribadong susi ng indibidwal ay hindi nakompromiso, ang mga digital na lagda ay maaaring magbigay ng lahat ng tatlong mga katangian na ito sa data.

Maaari kang magtataka kung bakit kailangan namin ang mga pag-aari na ito sa unang lugar. Bumalik tayo at pag-isipan kung paano natin ginagawa ang mga bagay sa harapan.

Sabihin natin na may utang ka sa iyong kaibigan na si Mike $ 100. Ikaw ay isang mabuting tao, kaya natutuwa kang bayaran siya kapag nakuha mo ang pera.

Ang pinakamahusay na paraan upang gawin ito ay ang pagbibigay lamang ng isang $ 100 bill kay Mike. Kilala mo siya nang maraming taon at alam mo kung ano ang hitsura niya, kaya magiging ganito madaling i-verify ang kanyang pagkakakilanlan at sa gayon patunayan na nagbibigay ka ng pera sa tamang tao.

Kung talagang anal ka, maaari mo ring suriin ang kanyang ID at gawin siyang mag-sign isang resibo ng sulat-kamay para sa iyo. Ang pirma sa resibo ay magbibigay ng integridad at gagawin itong hindi maitatatwa.

Paano kung sa halip na gawin ang transaksyon nang harapan, kumuha ka ng isang tawag mula sa isang tao na nagsasabing sila si Mike, at dapat kang magpadala ng $ 100 sa numero ng account na 12345678.

“Ngunit hindi ka tulad ni Mike,” sabi mo.

“May sipon ako. Ipadala ito ngayon, kailangan ko ang pera. “

Ipapadala mo ba ang pera? Hindi siguro.

Walang paraan upang malaman kung ito ba talaga ay si Mike o ang tamang numero ng account. Para sa lahat ng alam mo, maaaring ito ay isang impostor na nagsisikap na magnakaw mula sa iyo. Sa halip na mailipat kaagad ang pera, mas mainam na maghintay hanggang makita mo si Mike upang mabigyan mo siya nang personal.

Tulad ng sa itaas na senaryo, madalas kaming tumatakbo sa mga sitwasyon na kailangan natin i-verify ang pagkakakilanlan ng isang partido o ang integridad ng data sa online na mundo. Iyon ang dahilan kung bakit ang mga digital na lagda ay tumaas bilang isang mekanismo na maaaring magbigay ng mga pag-aari na ito at mapadali ang ligtas na mga transaksyon sa online.

Kung wala ang mga ito, maaaring hindi natin alam kung sino ang ating nakikipag-usap, hindi matiyak kung na-tampuhan ba o hindi ang data, at maaaring tanggihan ng tao na sila ay may pananagutan.

Ang paggamit ng mga pirma sa digital

Ang mga pag-aari ng mga digital na lagda ay nagbibigay sa kanila ng kapaki-pakinabang sa isang malawak na iba’t ibang mga application. Madalas silang ginagamit ng kanilang sarili o kasabay ng pag-encrypt sa isang hanay ng iba’t ibang mga protocol ng seguridad, tulad ng:

• IPsec
• SSH
• TLS

Madalas rin silang ginagamit sa pamamahala ng mga karapatan sa digital, sa teknolohiya ng blockchain, sa pamamahala ng kontrata mga aplikasyon, bilang bahagi ng pamamahagi ng software, at sa pananalapi.

Kasaysayan ng mga digital na lagda

Ang ideya ng mga digital na lagda ay unang inilutang ng mga kilalang cryptographers na sina Whitfield diffie at Martin Hellman sa kanilang 1976 na papel Bagong Direksyon sa Cryptography. Noong 1978, dinala nina Ronald Rivest, Adi Shamir at Len Adleman ang RSA algorithm sa pangmalas sa publiko, na maaaring magamit upang makagawa ng mga hindi secure na digital na lagda.

Ito ay tumagal ng isa pang dekada para sa mga digital na lagda upang lumitaw sa isang laganap na aplikasyon: ang paglabas ng IBM’s Lotus Notes 1.0. Mula noon, ang mga pirma ng digital ay nagsimulang makita ang mas malawak na pag-aampon habang lumitaw ang mga bagong pamamaraan at lumago ang pangangailangan para sa online na pagpapatunay at tseke ng integridad.

Isang maikling intro sa public-key na kriptograpiya

Bago tayo tumalon sa mga digital na lagda, mas mahusay na takpan ang ilan sa mga mahahalagang aspeto ng public key cryptography, na bumubuo ng batayan ng kung paano gumagana ang mga lagda ng digital.

Kung medyo bago ka sa krograpiya, ang system na mas pamilyar sa iyo ay simetriko-key encryption. Nangangahulugan lamang ito na ang parehong susi (na katulad ng isang password, ngunit may ilang pagkakaiba) ay ginagamit sa parehong pag-encrypt at decrypt data.

Ang pampublikong key na pag-encrypt ay isang rebolusyon, sapagkat kasangkot ito gamit ang magkakahiwalay na mga susi para sa proseso ng pag-encrypt at decryption, humahantong sa isang hanay ng mga iba’t ibang mga aplikasyon ng cryptographic. Ang dalawang susi na ito ay nabuo ng isang key na pares, na binubuo ng pampublikong susi at pribadong key. Ang pampublikong susi ay maaaring malinaw na ibinahagi sa publiko, habang ang pribadong susi ay dapat na itago nang lihim upang maging maayos ang system.

Ang dalawang pinaka-karaniwang gamit ng public-key na kriptograpiya ay ang pag-encrypt at mga pirma ng digital.

Pag-encrypt

Isa sa mga tampok ng groundbreaking ng pampublikong key kriptograpiya ay iyon pinapayagan nito ang mga partido na hindi pa nakikilala upang kumpiyansa na magpadala ng mga mensahe sa bawat isa. Hinahanap ng nagpadala ang pampublikong susi ng kanilang nais na tatanggap (ang mga ito ay matatagpuan sa mga pampublikong key server, sa mga personal na website, o sa pamamagitan lamang ng pagtatanong sa indibidwal), pagkatapos ay i-encrypt ang isang mensahe gamit ang key na ito, bago ipadala ito sa tatanggap.

Ang tatanggap ay ang tanging tao na maaaring ma-access ang mensahe – sa pag-aakalang ang pribadong susi ay hindi nakompromiso – sa pamamagitan ng pag-decryption nito sa kanilang pribadong key. Kahit na ang pampublikong susi ay ginamit upang i-encrypt ang mensahe, maaari lamang itong mai-decry ng pribadong key. Kung nais ng tumanggap na tumugon, nahanap nila ang pampublikong susi ng orihinal na nagpadala, pagkatapos ay ulitin ang proseso.

Tingnan din: Ipinaliwanag ang mga karaniwang uri ng pag-encrypt

Paano gumagana ang mga digital na lagda?

Tulad ng sinabi namin, ang mga pirma ng digital ay ginagamit para sa pagpapatunay, upang makita kung ang data ay na-tampered, at upang magbigay ng hindi pagtanggi. Mayroong isang hanay ng iba’t ibang mga mekanismo na maaaring magamit para sa mga digital na lagda, at ang bawat isa ay mayroon silang kaunting pagkakaiba-iba sa kung paano sila nakaayos.

Sa pangkalahatan, ang mga algorithm na ito ay kailangang binubuo ng tatlong sub-algorithm:

• Ang isang pangunahing algorithm ng henerasyon – Ang algorithm na ito ay bumubuo ng isang random key key para sa isang gumagamit. Ang mga numero na kasangkot sa mga pangunahing pares ay kailangang sumunod sa ilang mga parameter na maituturing na ligtas. Dalawa sa mga pinakamahalagang aspeto ay ang mga numero ay sapat na random at sapat na sukat.
• Isang algorithm para sa pag-sign data – Kapag ang isang gumagamit ay may kanilang mga susi, may mga tukoy na paraan para sa kung paano inilalapat ang mga ito sa data sa proseso ng pirma.
• Isang algorithm para sa pagpapatunay ng lagda – Gayundin, ang pagpapatunay ng isang lagda ay sumusunod sa isang paunang natukoy na proseso.

Para sa isang digital na sistema ng lagda upang maging epektibo, kailangan itong maayos sa isang paraan na:

• Ang data na nilagdaan gamit ang isang pribadong key ay na-verify gamit ang parehong pampublikong susi ng parehong indibidwal.
• Ito ay dapat na imposible imposible (gamit ang kasalukuyang teknolohiya at mga pamamaraan) upang makagawa ng isang wastong pirma nang hindi alam ang pribadong susi ng indibidwal.

Ang ilan sa mga pinaka-karaniwang mga digital na lagay ng scheme ay kinabibilangan ng RSA, DSA, EcDSA at EdDSA.

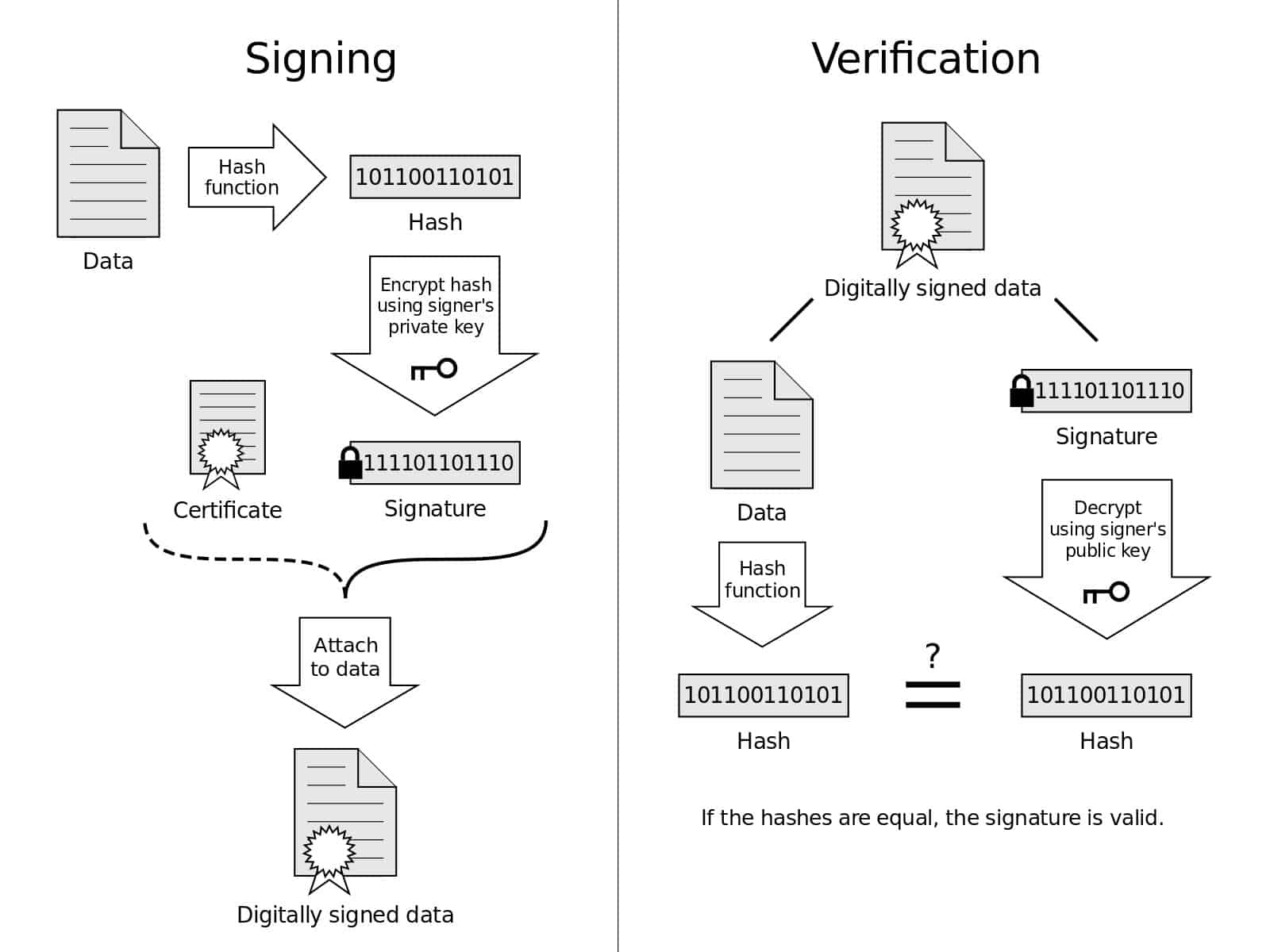
Ang imaheng ito ay nagbibigay ng isang visual na representasyon ng mga proseso ng pag-sign at pagpapatunay. Diagram ng Digital na Lagda sa pamamagitan ng lisensyado ng Acdx sa ilalim CC0

RSA

Ang RSA ay ang unang digital na algorithm ng pirma, ngunit maaari din itong magamit para sa pampublikong key na pag-encrypt. Sa artikulong ito, laktawan namin ang aspeto ng pag-encrypt, ngunit maaari mong malaman ang higit pa tungkol dito sa aming komprehensibong artikulo na sumasaklaw sa kung ano ang RSA at kung paano ito gumagana.

RSA pangunahing henerasyon

Sa ligtas na pagpapatupad ng RSA, ang mga pangunahing pares ay karaniwang awtomatikong maitatag sa ilalim ng sumusunod na proseso:

Punong henerasyon

Ang dalawang indibidwal na pangunahing numero ay napili, p at q. Ang eksaktong sukat ng mga prima na ito ay magkakaiba depende sa pangunahing sukat. Sa mga araw na ito, ang isang minimum na 2048-bit RSA key ay karaniwang inirerekomenda para sa sapat na seguridad, kaya pinag-uusapan natin ang tungkol sa dalawang punong numero na dumami upang makabuo ng isang 2048-bit na numero.

Ang 2048 bits ay isang sukat sa sistema ng binary number. Kung ang isang bilang ng laki na ito ay na-convert sa aming mas pamilyar na perpektong sistema, magiging halos mahaba ito:

790279459827301874397592846209502937592870495029380589710393

7019019209839375970193850891039510730584153687576287365984259

3824756984376582763487912837582736592873684273684728938575872

4958729873958729835792875982795837529876348273685729843579348

7958458720948602984912837502948019371092482793857928739548772

3975928375924785938670358103799581093750193850791345986792384

7378267352673547623568734869386945673456827659493849024875809

6039429837592834759348759384759284780634701938091803984091804

9810938592873995710901985013984019835091835019830910791803958

1039519039518093581093850198401935801938401983409180938510983

09180019

Ang mga primes sa RSA ay dapat mapili nang sapalaran at dapat magkaroon ng magkatulad na haba.

Sa aming halimbawa, gagamitin namin ang mas maliit na mga numero upang mas madaling maunawaan ang mga bagay. Magkaroon ng kamalayan na ang paggamit ng mga susi ng laki na ito ay gagawing maliit ang mga pirma sa digital. Ito ang dahilan kung bakit ang mga malalaking halaga ay ginagamit sa pagsasanay.

Sabihin natin na:

p = 13

q = 17

Ang unang hakbang ay upang makalkula ang modulus n gamit ang sumusunod na pormula:

n = pq

n = 13 x 17

n = 221

Ang halaga ng n din ang pangunahing haba.

Ang buong pag-andar ni Carmichael

Ngayon mayroon tayong halaga para sa n, ang susunod na hakbang ay ang paggamit ng ganap na pagpapaandar ni Carmichael:

λ(n) = lcm (p – 1, q – 1)

Mayroong ilang mga bagay na kailangan mong maunawaan:

• λ(n) ay nangangahulugang kumpleto si Carmichael para sa halaga ng n
• lcm ay kumakatawan sa pinakamababang karaniwang multiplier. Ito ang pinakamababang karaniwang bilang na pareho p-1 at q-1 maaaring hatiin sa

I-plug ang aming mga numero sa equation:

λ(221) = lcm (13 – 1, 17 – 1)

λ(221) = lcm (12, 16)

Kung ikaw ay magaling sa matematika sa kaisipan, maaaring naiisip mo iyon 48 ay ang pinakamababang karaniwang multiplier ng pareho 12 at 16. Ito ay dahil ang 48 ay ang pinakamaliit na bilang na maaaring kapwa magkasama sa (12 x 4 = 48, 16 x 3 = 48). Samakatuwid:

λ(221) = 48

Pagdating sa pampublikong susi

Sa RSA, ang pampublikong susi ay binubuo ng halaga n (na kung saan namin na kinakalkula bilang 221) at e. Dahil ang pampublikong susi ay malayang ibinahagi, ang halaga para sa e hindi kailangang maging lihim. Sa katunayan, madalas itong nakatakda sa 65,537 sa pagsasagawa, dahil ang mas malaking bilang ay babagal ang proseso ng pag-encrypt. Sa aming halimbawa, magtakda kami e hanggang 5, para lamang gawin itong isang maliit at simpleng bilang upang gumana.

Samakatuwid, ang pampublikong susi para sa halimbawang ito ay binubuo ng 221 at 5. Sakupin namin ang mga detalye kung paano inilalapat ang pampublikong susi sa mga sumusunod na seksyon.

Ang pagguhit ng pribadong susi

Tulad ng aming pampublikong susi ay binubuo ng dalawang numero, gayon din ang aming pribadong susi. Ang mga pribadong key ay binubuo ng d at e. Alam na natin ang halaga para sa e (5), at maaari naming gamitin ang sumusunod na pormula upang mahanap d:

d = 1 /e mod λ(n)

Tandaan na mod sumisimbolo lamang ng isang operasyon ng modulo, na karaniwang nangangahulugang kailangan mong hanapin ang nalalabi kapag nahati mo ang kaliwang bahagi sa kanan. Bilang halimbawa:

17 mod 3 = 2

Ito ay dahil ang 3 ay umaangkop sa 17 sa kabuuan ng 5 beses, na may natitirang 2.

Medyo naiiba ang aming halimbawa. Ang “1 /e mod“Ang segment ng ekwasyon ay maaaring mukhang nagsasabi sa iyo na hatiin 1 ni e, ngunit hindi talaga. Nakakalito, ngunit ito ay isang paraan ng kinatawan ng modular na kabaligtaran. Ang equation ay talagang sinasabi sa amin upang makalkula ang modular na kabaligtaran ng e at λ(n).

Ang modular na kabaligtaran ay karaniwang nagmula gamit ang pinalawak na Euclidean algorithm, ngunit hindi namin tatakpan iyon sa artikulong ito. Sa halip, gagamitin lamang namin ang isang online calculator upang gawing mas madali ang mga bagay.

Ngayon na natagpuan natin iyon, ipasok natin ang aming mga halaga sa pormula:

d = 1/5 mod 48

Hanapin d, ang kailangan lang nating gawin ay ipasok ang ating halaga para sa e (5) sa online calculator kung saan sinasabi nito integer, pagkatapos ang aming halaga para sa λ(n), na kung saan 48, kung saan sabi nito modulo.

Nagbibigay ito sa amin ng isang resulta ng 29 ayon sa online calculator. Samakatuwid, ang aming pribadong key ay binubuo ng:

e = 5

d = 29.

Ngayon na nabuo namin ang pareho sa aming mga susi, ang susunod na tanong ay, “Ano ang gagawin natin sa kanila?” Kaya, maaari naming gamitin ang mga ito upang i-encrypt at i-decrypt ang mga mensahe sa pamamagitan ng public-key na kriptograpiya, ngunit ang artikulong ito ay tungkol sa mga digital na lagda, kaya tutukan natin ito.

Digit na pag-sign ng data sa RSA

Sabihin nating may isang taong nais magpadala ng isang mensahe sa kanilang kaibigan, ngunit nais nilang tiyakin na ma-verify ng kaibigan ang pagiging tunay at integridad ng mensahe. Magagawa nila ito sa pamamagitan ng paggamit ng isang pirma digital RSA upang mag-sign ang mensahe.

Ang unang hakbang ay patakbuhin ang buong mensahe sa pamamagitan ng isang function na hash. Ang mga ito ay mga one-way function na palaging naghahatid ng parehong output para sa isang naibigay na input. Ang ligtas na pag-andar ng hash ay mahalagang imposible upang baligtarin, na nangangahulugan na ang output ay hindi maaaring magamit upang malaman ang input. Hindi rin maiiwasan para sa dalawang magkahiwalay na mensahe na magkaroon ng parehong output.

Maaari mong malaman ang higit pa tungkol sa hash function sa Ano ang nakakainis? Seksyon ng aming artikulo, Encryption, hashing, salting – ano ang pagkakaiba?

Sabihin natin na nais naming lagdaan ng digital na mensahe ang “Ito ay mainit ngayon“Upang ang aming tatanggap ay maaaring malaman kung ang mensahe ay tunay o hindi at kung ito ay nai-tampered sa. Kaya tatakbo kami “Ito ay mainit ngayon“Sa pamamagitan ng isang hash function.

Ang pag-unawa sa hash function

Sa mga araw na ito, ang pinakakaraniwang ginagamit na ligtas na hash function ay SHA-256. Kapag inilagay namin ang aming mensahe sa pamamagitan ng isang online na calculator ng SHA-256, nagbibigay ito sa amin ng isang resulta tulad nito:

efbcf22b4cd04d49daa87cfbda7d2313cc665c35bc9e18954af16c104a731952

Nagtaas ito ng ilang mga problema para sa aming halimbawa. Ang una ay hindi ito bilang isang perpektong bilang tulad ng nakasanayan ng karamihan sa mga tao. Maaaring napansin mo na mayroong mga liham sa bilang na ito, at dumadaloy lamang sila f. Nagbibigay ito sa amin ng isang pahiwatig na ito ay talagang isang hexadecimal number.

Ang ang hexadecimal system ay nakasalalay sa isang base ng 16, sa halip na isang base ng 10, tulad ng number system na karaniwang ginagamit natin. Nangangahulugan ito, na sa halip na pagbilang sa maraming mga 10, binibilang ito sa maraming mga 16, at ang unang 6 na titik ng aming alpabeto ay ginagamit upang gumawa ng mga dagdag na bilang. Ang bilang na tulad nito ay maaaring ma-convert sa aming pang-araw-araw na sistema ng desimal, ngunit wala sa saklaw ng artikulong ito.

Ang pangalawang isyu na mayroon tayo ay ito ay isang malaking bilang. Kung ito ay na-convert sa desimal, mas mahaba pa. Dahil naglalayong kami para sa pagiging simple sa gabay na ito, ang pagpapatakbo ng mga kalkulasyon na may tulad na isang malaking bilang ay nakakagawa ng mga bagay na masyadong nakalilito upang makuha ang mga pangunahing konsepto sa buong.

Sa ideya ng pagpapakita kung paano gumagana ang mga pirma ng digital na RSA sa paraang madaling maunawaan, hindi namin gagamit ng ganoong malaking halaga ng hash sa sumusunod na halimbawa. Sa halip, magpapanggap tayo na ang hash na halaga ng “Ito ay mainit ngayon“Ay simple 10.

Kailangan din nating magpanggap, na tulad ng anumang tunay na hash, tuwing inilalagay namin ang aming input ng “Ito ay mainit ngayon” sa pamamagitan ng hash function, ito ay palaging ibabalik ang halaga ng 10. Upang maging kaayon sa kung paano normal na gumana ang hash function, kakailanganin nating magpanggap na hindi kapani-paniwalang imposible para sa anumang ibang input na magbigay ng parehong halaga. Katulad nito, kailangan nating magpanggap na hindi rin posible na malaman ang aming orihinal na pag-input mula sa halagang ito. Ang mga pag-aari na ito ay kung ano ang gumawa ng labis na kapaki-pakinabang na hashes.

Paano ginagamit ang pribadong key ng nagpadala upang awtomatikong lagdaan ang hash value

Ang aming nagpadala ay nai-type ang kanilang mensahe, pagkatapos ay ilagay ito sa pamamagitan ng isang pag-andar ng hash, na pinapanggap namin na ibinalik ang isang halaga ng 10. Kapag ang nagpadala ay may sagabal ng mensahe, maaari silang lumikha ng digital na lagda sa pamamagitan ng paglalapat ng kanilang pribadong key sa hash na halaga gamit ang sumusunod na pormula:

m (c) = cd mod n

Ito talaga ang pormula para sa decrypting data na naka-encrypt sa pampublikong susi ng tatanggap, ngunit ginagamit din ito para sa mga digital na pag-sign dokumento.

Pagdating sa digital na lagda:

• Ang halaga ng m (c) ang magiging pirma.
• Ang halaga ng c ay ang pag-abala ng mensahe (10).
• Ang halaga ng d ay bahagi ng pribadong susi ng nagpadala, na nakuha namin nang mas maaga (29).
• Ang mod ang pag-andar ay ang parehong natitirang operasyon na nasakop namin nang mas maaga.
• Ang halaga ng n ay ang iba pang bahagi ng pribadong susi ng nagpadala, na kinakalkula namin sa simula (221).

Kaya, ilagay natin ito sa aming pormula:

m (c) = 1029 mod 221

    m (c) = 100,000,000,000,000,000,000,000,000,000,000 mod 221

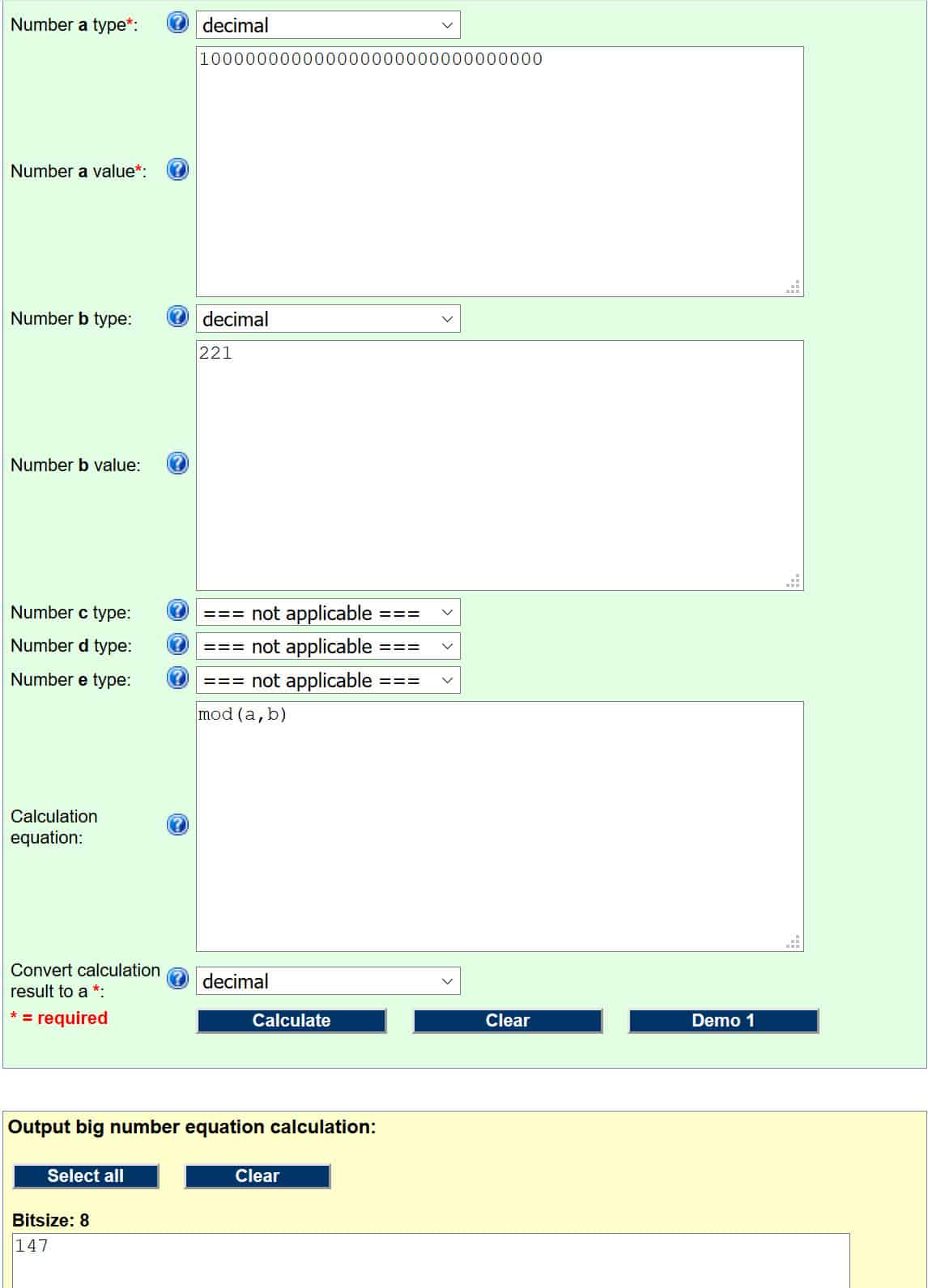
Patakbuhin ito sa mga sumusunod na modulo calculator (ipinaliwanag namin kung paano gumagana ang mga operasyon sa ilalim ng Ang pagguhit ng pampublikong susi seksyon). Para gumana ito nang maayos, kailangan nating itakda ang aming mga input bilang:

• Bilang a uri – desimal
• Bilang a halaga – 100000000000000000000000000000
• Bilang b uri – desimal
• Bilang b halaga – 221
• Pagkalkula ng pagkalkula (ito ay lamang ang code na nagsasabi sa calculator kung aling operasyon ang gumanap. Ito at iba pang mga code ay matatagpuan sa webpage na naka-link sa itaas ng seksyon ng pag-input) – mod (a, b)

Kung nagawa mo nang maayos ang mga bagay, dapat ganito ang hitsura:

Ang bilang sa dilaw na kahon ay ang aming sagot, kaya ang digital na lagda para sa hash ng mensahe ay 147.

Upang patunayan ang pagiging tunay at integridad ng mensahe, kasama ang pagbibigay ng hindi pagtanggi, ipapadala ng aming nagpadala ang mensahe “Ito ay mainit ngayon“Kasama ang digital na lagda ng 147 sa kanilang nais na tatanggap. Tandaan lamang na ginamit namin ang isang maliit na halaga para sa hash upang gawing simple ang mga bagay, sa halip na ang tunay na hadh ng mensahe.

Pag-verify ng mga pirma sa digital

Ang mga pirma ng digital ay kapaki-pakinabang lamang kung mapatunayan namin kung lehitimo ito. Hangga’t hindi nai-kompromiso ang pribadong key ng nagpadala, ang pagsubok ay maaaring subukan kung ang isang mensahe ay tunay at pinapanatili ang integridad sa pamamagitan ng paglalapat ng sumusunod na pormula sa digital na lagda:

    c (m) = me mod n

Sa isang baligtad ng proseso ng pag-sign, ito talaga ang pormula na ginagamit upang i-encrypt ang data sa RSA. Kapag ginagamit namin ang formula na ito upang i-verify ang mga lagda:

• Ang halaga ng c (m) ay magiging halaga ng hash ng nagpadala sa oras na nilagdaan nila ito (dahil sa istraktura ng RSA public-key algorithm, ang paglalapat ng pampublikong susi ng nagpadala sa pamamagitan ng pormula na ito ay aalisin ang operasyon ng pagpirma na ating gumanap, na nag-iwan sa amin ng aming orihinal na nagpapanggap na hash ).
• Ang halaga ng m ay ang digital na pirma (147).
• Ang halaga ng e ay bahagi ng pampublikong susi ng nagpadala, na nakuha namin nang mas maaga (5).
• Ang mod ang pag-andar ay ang parehong natitirang operasyon na nasakop namin nang mas maaga.
• Ang halaga ng n ay ang iba pang bahagi ng pampublikong susi ng nagpadala, na kinakalkula namin sa simula (221).

Itapon natin ang lahat sa formula:

    c (m) = 1475 mod 221

    c (m) = 68,641,485,507 mod 221

Gumamit ng parehong modulo calculator tulad ng dati at panatilihin ang lahat ng pareho, maliban sa:

• Bilang a halaga – 68,641,485,507

Kung naipasok mo nang tama ang mga bagay, dapat kang makakuha ng isang resulta ng:

c (m) = 10

Ngayon na ang tatanggap ay kinakalkula ang hash na halaga mula sa digital na lagda, ang kanilang susunod na hakbang ay upang makalkula ang hash na halaga ng mensahe na kanilang natanggap, “Ito ay mainit ngayon“. Kung natatandaan mo mula pa noong una, hindi talaga namin ginagamit ang totoong SHA-256 hash ng mensahe, dahil ang bilang ay magiging napakalaki at ginawang kumplikado ang halimbawa.

Sa halip, nagpapanggap na ang function ng hash ay talagang nagbigay sa amin ng maliit na bilang, 10, para sa aming input. Dahil ang mga function ng hash ay palaging naglalabas ng parehong resulta para sa isang naibigay na input, kapag inilalagay ng aming tatanggap “Ito ay mainit ngayon“Sa pamamagitan ng aming haka-haka na function na hash, matatanggap din nila ang halaga ng 10.

Ang proseso ng pag-verify ng pirma ay nagreresulta sa dalawang mga halaga. Ang unang halaga ay ang hash tulad ng kung ang digital na nagpadala ay awtomatikong nilagdaan ito ng kanilang pribadong susi. Kinakalkula namin ito sa itaas gamit ang pampublikong susi ng nagpadala.

Ang pangalawang halaga ay ang hadh ng mensahe na natanggap ng tatanggap. Ito ay kinakalkula sa pamamagitan ng paggamit ng parehong function na hash na ginamit ng nagpadala upang sumira sa kanilang orihinal na mensahe. Ang dalawang mga halagang ito ay ihahambing, at kung ang mga halaga ay magkapareho, kung gayon maaari nating isipin na ang mensahe ay tunay, pinapanatili ang integridad nito, at ito ay hindi maikakaila. Siyempre, ipinapalagay nito na ang pribadong susi ng nagpadala ay hindi nakompromiso.

Dahil ang aming halimbawa ay nagbalik ng isang halaga ng 10 para sa hash kapag ito ay nilagdaan ng nagpadala, pati na rin ang isang halaga ng 10 bilang hadh ng mensahe na natanggap, maaari nating isipin na ang mensahe, “Ito ay mainit ngayon ay nagmula sa taong sinasabing nagpadala nito, at hindi pa ito nabago mula nang ipinadala ito.

Kung nais ng tumatanggap na tumugon upang ma-verify ng kanilang susurender ang kanilang mensahe sa parehong paraan, paulit-ulit ang buong proseso, maliban sa mga pribado at pampublikong mga susi ay ginagamit para sa mga proseso ng pag-sign at pagpapatunay, ayon sa pagkakabanggit..

Ang lahat ng matematika na ito ay maaaring maalis sa iyo ang buong ideya ng mga digital na lagda. Huwag kang mag-alala, dahil ang pagpapatupad ng RSA ay awtomatiko ang prosesong ito, kaya hindi mo na kailangang mabulok ng anumang mga numero.

RSA pros & kahinaan

Ang RSA ay isa sa mga pinaka-malawak na suportado at ipinatupad digital algorithm algorithm, bagaman mayroong isang hakbang patungo sa mas bago, mas mahusay at ligtas na mga algorithm tulad ng ECDSA at EdDSA.

Kung ihahambing sa DSA (na tatalakayin namin sa susunod na seksyon), ang RSA ay mas mabilis sa pag-verify ng mga pirma, ngunit mas mabagal sa pagbuo ng mga ito. Dahil ang mga lagda ay madalas na nilikha nang isang beses at napatunayan nang maraming beses, ang RSA ay karaniwang ginustong sa DSA.

DSA

Ang seguridad ng Digital Signature Algorithm ay batay sa dalawang konseptong matematika, ang diskrete na logarithm na problema, at ilang mga katangian ng modular exponentiation. Para sa ilang mga grupo, walang kakayahang makalkula ang kanilang discrete logarithms sa kasalukuyang mga pamamaraan at teknolohiya.

Pangunahing henerasyon ng DSA

Upang makabuo ng mga susi ng DSA, ang unang hakbang ay ang pumili ng mga parameter na maaaring magamit ng isang pangkat ng mga gumagamit sa parehong system upang makabuo ng isang key na pares.

Bumubuo ng mga parameter

• Pagpili ng a function na hash – Ang SHA-256 ay ang pinaka-karaniwang pagpipilian upang matugunan ang mga kinakailangang modernong seguridad.
• Pag-aayos sa mga mahahalagang haba, L at N – Sa mga araw na ito, L dapat na hindi bababa sa 2,048 bits ang haba, habang N ay dapat na hindi bababa sa 256 bit.
• Magpasya sa isang kalakasan, q, iyon ang parehong haba ng N.
• Pumili ng isang kalakasan, p, saan p-1 ay isang maramihang ng q.
• Pumili ng isang numero, g, gamit ang sumusunod na pormula (kung saan h ay isang di-makatwirang bilang sa pagitan ng 1 at p-1):

g = h(p – 1) /q mod p

Karaniwan, ang mga halagang ito ay napakalaking numero upang mai-secure ang algorithm. Upang mapanatili ang aming halimbawa mula sa pagiging mahirap na makalkula o ipaliwanag, gagamitin namin ang mas maliit na mga numero na hindi talaga magiging ligtas. Sabihin natin na:

    q = 5

    p = 11

Hanapin g, isinasaksak namin ang aming mga numero sa formula. Gagamitin natin 3 bilang aming halaga para sa h:

g = 3 (11-1) / 5 mod 11

g = 32 mod 11

g = 9 mod 11

Gagamitin namin ang parehong calculator modulo tulad ng sa Paano ginagamit ang pribadong key ng nagpadala upang awtomatikong lagdaan ang hash value seksyon. Ang mga parameter ay magiging pareho, maliban sa:

• Bilang a halaga – 9
• Bilang b halaga – 11

Kung naipasok mo nang tama ang lahat, bibigyan ka nito ng isang resulta para sa g ng 9.

Bumubuo ng mga susi ng gumagamit

Kinuha ng mga indibidwal na gumagamit ang mga parameter na ito at gamitin ang mga ito upang mabuo ang kanilang pangunahing pares:

• Ang pribadong susi (x) ay isang numero sa pagitan 0 at q, na itinakda namin sa 5. Para sa aming halimbawa, pipiliin namin 2 upang maging x, ang aming pribadong susi.
• Ang pampublikong susi (y) ay kinakalkula gamit ang sumusunod na formula:

    y = gx mod p

Samakatuwid:

y = 92 mod 11

y = 81 mod 11

Gagamitin namin muli ang parehong calculator modulo. Ang mga parameter ay magiging pareho, maliban sa:

• Bilang a halaga – 81
• Bilang b halaga – 11

Kung naipasok mo nang tama ang mga bagay, dapat ay nakakuha ka ng isang resulta ng y = 4. Ang pampublikong susi ay samakatuwid 4.

Ngayon na nabuo namin ang lahat ng aming mga halaga, bigyan ka agad ng mabilis. Ang mga parameter para sa system ay:

• p = 11
• q = 5
• g = 9

Ang aming pangunahing pares ay binubuo ng:

• Ang pribadong susi, x = 2
• Ang susi ng publiko, y = 4

Digit na pag-sign ng data sa DSA

Maaaring gamitin ng mga nagpadala ang kanilang pribadong key ng DSA upang awtomatikong mag-sign data, na nagbibigay-daan sa kanilang tatanggap upang mapatunayan kung ang mensahe ay tunay at pinapanatili ang integridad nito. Pinipigilan din nito ang nagpadala sa pagtanggi sa mensahe.

Ang proseso ng pirma ay nagsisimula sa pamamagitan ng pagbuo ng isang random na halaga k, na nasa pagitan 1 at q. Para sa halimbawang ito, pumili lang tayo 3 bilang aming “random” na numero, k.

Sinusunod namin ang sumusunod na pormula upang lumikha ng isang indibidwal na susi (r) para sa mensahe:

r = (gk mod p) mod q

Itapon natin sa aming mga numero:

r = (93 mod 11) mod 5

r = (729 mod 11) mod 5

Ginagamit namin muli ang aming mode ng calculator, pagpasok 729 at 11, na nagbibigay sa amin ng isang resulta ng 3. Samakatuwid:

r = 3 mod 5

At pagkatapos ay ulitin namin muli ang operasyon ng modulo kasama ang mga bagong halaga upang maibigay sa amin:

r = 3

Ang aming halaga para sa r ay ginagamit bilang susi para sa mensahe.

Dumating kami kasama ang iba pang bahagi ng digital na lagda, s, gamit ang sumusunod na pormula:

s = k-1(H(m) + xr) mod q

Ang k-1 ay hindi kumakatawan sa pagkuha ng negatibong kapangyarihan ng k, ngunit sa halip na kinakalkula ang modular na kabaligtaran, tulad ng sa ating Nailalarawan ang pribadong key subseksyon sa naunang bahagi ng artikulo kung saan napag-usapan namin ang tungkol sa RSA.

H(m) ang halaga ng hash para sa mensahe na pinirmahan ng nagpadala. Karaniwan, ito ay isang mahabang halaga ng hash na nagmula sa mensahe, tulad ng sa Ang pag-unawa sa mga halaga ng hash subseksyon sa itaas, na kung saan namin sakop kapag pinag-uusapan namin ang tungkol sa RSA algorithm.

Para sa halimbawang ito, panatilihin nating simple ang mga bagay. Tulad ng sa RSA section, sasabihin namin na ang aming mensahe, m, ay “Ito ay mainit ngayon“ at ang hadh ng mensahe H(m), ay 10.

Kaya’t ipasok natin ang lahat ng aming mga halaga sa pormula:

s = 3-1 (10 + 2 x 3) (mod 5)

s = 3-1 (10 + 6) (mod 5)

s = 3-1 (16) (mod 5)

Ngayon, kukuha kami ng modular na kabaligtaran ng 3 para sa pagkakasunud-sunod ng 5 (dahil 5 ang aming halaga para sa q), gamit ang parehong modular kabaligtaran calculator mula sa mas maaga. Ipasok 3 bilang integer at 5 bilang modulo, na magbibigay sa iyo ng isang resulta ng 2. Samakatuwid:

s = 2 (16) (mod 5)

s = 32 (mod 5)

Bumalik tayo sa aming calculator para sa normal na operasyon ng modulo, na pinapanatili ang parehong mga parameter na ginamit namin kanina, maliban sa:

• Bilang a halaga – 32
• Bilang b halaga – 5

Kung ginawa mo ito nang tama, magbibigay ito ng isang halaga para sa s ng 2. Ang digital na pirma ay binubuo ng r at s (3 at 2, ayon sa pagkakabanggit). Ang mga nagpadala ay nagpapadala ng digital na pirma sa kanilang tatanggap kasama ang kanilang mensahe, “Ito ay mainit ngayon“. Ibabahagi din nila ang mga halaga ng p, q, g at y kasama ang kanilang tatanggap.

Pag-verify ng mga pirma sa digital

Kapag natanggap ng tatanggap ang digital na pirma sa tabi ng mensahe, maaari nilang i-verify ang integridad at pagiging tunay ng mensahe sa mga sumusunod na hanay ng mga kalkulasyon.

Ang unang hakbang ay upang mahanap ang hash ng mensahe na kanilang natanggap. Ginagawa ito ng tatanggap sa pamamagitan ng pagpapatakbo ng buong mensahe sa pamamagitan ng isang function na hash. Upang panatilihing simple at pare-pareho ang mga bagay, sabihin nating ang abala ng mensahe, H(m) ay 10.

Ang tatanggap ay ipinadala din ng mga sumusunod na halaga, na ginagamit nila sa proseso ng pag-verify:

• Ang digital na pirma (r, s) – 3, 2
• p – 1
• q – 5
• g – 9
• y – 4

Ang unang pagkalkula ay upang mahanap w:

w = s-1 mod q

Muli, ang s-1 ay kumakatawan sa pagkuha ng modular na kabaligtaran. Ipasok natin ang aming mga halaga:

w = 2-1 mod 5

Gagamitin namin ang modular kabaligtaran calculator mula sa mas maaga. Ipasok 2 bilang integer at 5 bilang modulo, na magbibigay sa iyo ng isang resulta ng 3 para sa w. Ang susunod na hakbang ay upang mahanap u1 kasama ang sumusunod na formula:

u1 = H(m) x w mod q

Itapon natin ang aming mga halaga:

u1 = 10 x 3 mod 5

u1 = 30 mod 5

Bumalik sa normal na calculator ng modulo, na pinapanatili ang parehong mga parameter na ginamit namin nang una, maliban sa:

• Bilang a halaga – 30
• Bilang b halaga – 5

Nagbibigay ito sa amin ng isang resulta ng 0 para sa u1.

Ginagamit namin ang susunod na formula upang makabuo u2:

u2 = r x w mod q

Ipasok natin ang aming mga numero:

u2 = 3 x 3 mod 5

u2 = 9 mod 5

Pagkatapos ay bumalik kami sa normal na calculator ng modulo, gamit ang parehong mga parameter tulad ng mas maaga, maliban sa:

• Bilang a halaga – 9
• Bilang b halaga – 5

Kung ipinasok mo ito nang tama, bibigyan ka nito ng isang resulta para sa u2 ng 4.

Ngayon mayroon tayong mga halaga para sa u1 at u2, maaari naming mahanap ang v, gamit ang sumusunod na pormula:

v = (gu1yu2 mod p) mod q

Itapon natin sa aming mga numero:

v = (90 x 44 mod 11) mod 5

v = (1 x 256 mod 11) mod 5

v = (256 mod 11) mod 5

Bumalik kami sa aming normal na modulo calculator, gamit ang parehong mga parameter tulad ng mas maaga, maliban sa:

• Bilang a halaga – 256
• Bilang b halaga – 11

Nagbibigay ito sa amin ng isang resulta ng 3. Samakatuwid:

v = 3 mod 5

Pagkatapos ay ginagamit namin ang normal na calculator ng modulo sa isang pangwakas na oras, muli kasama ang parehong mga parameter, maliban sa:

• Bilang a halaga – 256
• Bilang b halaga – 11

Nagbibigay ito sa amin ng isang resulta para sa v ng 3.

Kung ang mensahe ay tunay at hindi na-tampered, pagkatapos magiging v ang pantay sa r:

    v = 3

    r = 3

    3 = 3

Samakatuwid ang mensahe ay ipinadala ng may-ari ng pribadong key, at ang mensahe ay hindi nabago mula nang ito ay naka-sign.

Pros ng DSA & kahinaan

Ang seguridad ng DSA ay nakasalalay sa kung gumagamit ba ito ng sapat na numero. Karagdagan sa p, q at g pagsunod sa tamang mga parameter, ang halaga ng k kailangan ding maging random. Hindi ito dapat maging mahuhulaan na halaga, o isang halaga na ginagamit nang maraming beses. Kung ang mga kinakailangang ito ay hindi natutugunan, pagkatapos ang susi ay maaaring mabawi ng isang umaatake.

Sa kabila ng posibilidad na ito, Ang DSA ay karaniwang itinuturing na ligtas hangga’t ito ay ipinatupad nang tama at gumagamit ito ng sapat na mga halaga. Kahit na medyo ligtas ito, ang DSA ay hindi malamang na maipatupad kumpara sa RSA o sa iba pang mga digital na pamamaraan ng lagda. Kung ihahambing sa RSA, maaari itong makabuo ng mga susi nang mas mabilis at mas mabilis din sa pagbuo ng mga digital na lagda, ngunit mas mabagal sa pag-verify ng mga ito.

Ang Bersyon 7.0 ng OpenSSH ay tumigil sa pagsuporta sa mga susi ng DSA nang default, na tila isang senyas na ang mundo ay lumilipas sa nakaraang DSA at sa iba pang mga algorithm.

ECDSA & EdDSA

Ang RSA at DSA ay hindi lamang ang mga digital na algorithm algorithm, at hindi rin sila ang pinaka-angkop para sa lahat ng mga sitwasyon. Mayroong isang hanay ng iba pa, tulad ng ECDSA at EdDSA, na may mga pag-aari na ginagawang mas kanais-nais sa ilang mga sitwasyon.

Sa kasamaang palad, ang mga ito ay umaasa sa mas kumplikadong matematika, tulad ng elliptic curve at Edwards curve cryptography. Hindi namin tatakpan ang mga ito nang detalyado ngayon dahil sa dagdag na pagiging kumplikado, ngunit pag-uusapan natin ang ilan sa kanilang mga potensyal na positibo at negatibo.

ECDSA

Ang Elliptic curve Digital Signature Algorithm ay isang pagkakaiba-iba ng DSA na nagsasama ng elliptic curve cryptography. Nagbibigay ito ng isang katulad na antas ng seguridad sa RSA, ngunit may isang mas maliit na susi. Ginagawa nitong mas mahusay kaysa sa RSA o DSA sa karamihan ng mga aspeto ng pagganap.

EdDSA

Ito ay isa pang alternatibong DSA, maliban na ito ay batay sa mga curves ng Twisted Edwards. Ito ay medyo bago hanggang sa pumunta ang mga algorithm, na kung saan ay may parehong mga pakinabang at kawalan nito. Sa positibong panig, gumagamit ito ng mga mas bagong pamamaraan na nagdaragdag sa pagganap nito.

Sa kasamaang palad, ang mga mas bagong algorithm ay hindi nalantad sa masusing pagsisiyasat, kaya maraming mga tao ang nag-iingat kapag nagpapasya kung ipatupad o ipatupad ang mga ito.

Sa kabila nito, ang paggamit ng Nagbibigay ang EdDSA ng isang mataas na antas ng pagganap, paglaban sa mga pag-atake sa gilid, at nawawala ang pangangailangan para sa isang natatanging random na numero sa bawat pirma. Sa yugtong ito, ang EdDSA ay mukhang nangangako at nagsisimula itong makita ang mas malawak na pagpapatupad, ngunit kailangan nating maghintay at makita kung ang mga pag-aaral sa hinaharap ay nakakahanap ng anumang mga butas sa seguridad.

Mga digital na sertipiko

Kahit sino ay madaling gumawa ng isang key pares, kahit na isang mang-aatake. Kaya kung ano ang nagpipigil sa isang tao na gumawa ng isang bungkos ng mga susi at pagpapanggap na sila ang Pangulo, o posing tulad ng sinumang iba pa?

Buweno, walang humihinto sa isang tao na mag-angkin na sila ay ibang tao, ngunit may isang sistema sa lugar na nagpapahintulot sa iba na matukoy kung ang tunay na tao ay ang kanilang inaangkin na. Ito ay tinatawag na pampublikong susi ng imprastraktura (PKI), at nagsasangkot ito mga digital na sertipiko na nag-uugnay sa pampublikong susi ng isang indibidwal o entidad sa kanilang tunay na pagkakakilanlan. Ang mga sertipiko na ito ay nilagdaan ng iba upang ipahiwatig kung gaano karaming dapat kumpiyansa ang sertipiko.

Maaari mong ihambing ang proseso sa paggamit ng mga notaryo upang i-verify ang mga dokumento. Kung ang isang tao ay may isang kopya ng isang sertipiko ng kapanganakan, maaari kang mag-alinlangan tungkol sa kung ito ay lehitimo. Kung ang parehong sertipiko ng kapanganakan ay nilagdaan at naselyohan ng isang notaryo, mas malamang na maniwala ka na ito ay isang tunay na kopya.

Bakit?

Sapagkat ang lagda at selyo ay nagpapakita na ang isang pinagkakatiwalaang pampublikong entidad ay nakakita sa indibidwal at sa kanilang orihinal na sertipiko ng kapanganakan, pagkatapos ay napatunayan na ang kopya ay sa katunayan lehitimo. Pinatunayan ng notaryo ang kopya ng sertipiko ng kapanganakan at pinanatili ang kanilang reputasyon sa likod nito gamit ang kanilang pirma at selyo.

Ang tiwala na mayroon kami para sa notaryo ay ililipat sa kopya ng sertipiko ng kapanganakan, na nagpapahintulot sa amin na mapagkakatiwalaan ito nang higit pa kaysa sa isang na hindi napapansin.

Mayroong dalawang pangunahing uri ng sertipikasyon, cmga awtoridad ng ertigned (CA) at web ng tiwala.

Mga awtoridad sa sertipiko

Ang mga awtoridad sa sertipiko ay pinagkakatiwalaang mga organisasyon na nagpapatakbo ng mga tseke sa mga indibidwal o mga nilalang upang mapatunayan kung sila ang lehitimong may-ari ng isang pampublikong susi. Kung isiniwalat ng mga tseke na ang indibidwal ay ang tunay na may-ari, kung gayon ang awtoridad ng sertipiko ay pipirma ang sertipiko gamit ang sariling susi, na nagpapahiwatig na nakumpleto nito ang tseke at naniniwala na ang indibidwal at pampublikong susi ay lehitimong nauugnay.

Hangga’t pinagkakatiwalaan namin ang awtoridad ng sertipiko at ang kanilang proseso ng pagpapatunay ng susi, pagkatapos ay mapagkakatiwalaan namin ang isang sertipiko na nilagdaan ng mga ito, at sa gayon na ang susi ng publiko ay tunay na kumakatawan sa indibidwal na iyon.

Depende sa uri ng sertipiko at ang aplikasyon nito, ang iba’t ibang mga antas ay maaaring magkakaiba-iba ng mga proseso ng pag-verify, at sa gayon ang alinman ay kumakatawan sa isang mas mataas o mas mababang antas ng pagtitiwala.

Ang web ng tiwala

Ang web ng tiwala ay nagpapatakbo sa ilalim ng isang katulad na saligan, maliban sa tdito walang mga gitnang katawan tulad ng mga awtoridad sa sertipiko na nagsasagawa ng proseso ng pag-verify at pumirma sa mga sertipiko.

Sa halip, ang web ng tiwala ay nakasalalay sa iba pang mga indibidwal upang mag-sign ng mga sertipiko, at ang kanilang reputasyon sa link sa pagitan ng indibidwal at pampublikong susi. Ang sistemang ito ay kadalasang ginagamit sa PGP, kung saan ang mga gumagamit ay madaling gumawa ng kanilang sariling mga sertipiko.

Ito ay gumagana tulad nito:

Sabihin nating mayroon kang dalawang kaibigan na nais ang kanilang mga sertipiko ay nilagdaan upang patunayan na sila ang mga lehitimong may-ari ng kani-kanilang mga susi sa publiko. Kilala mo nang mabuti ang mga taong ito, at ipinakikita nila sa iyo ang kanilang mga ID ng gobyerno, na tinitiyak mong tiyak na sila ang mga sinasabi nila, at sa gayon ay ang tunay na mga may-ari ng pampublikong mga susi na kanilang inaangkin.

Dahil alam mo na ang mga ito ay lehitimong may-ari ng kanilang mga pampublikong susi, natutuwa mong gamitin ang iyong pribadong key upang mag-sign ang kanilang mga sertipiko, isinasapuso ang iyong reputasyon at mahalagang sabihin na “Oo, napatunayan ko ang mga pagkakakilanlan ng mga indibidwal na ito at sila ay inaangkin nila na “. Ang dalawang magkakaibigan na ito ay maaaring gawin ang parehong sa iyo.

Sabihin natin na ang bawat isa sa iyong dalawang kaibigan ay may dalawang iba pang mga kaibigan na nais nilagdaan ang kanilang mga sertipiko. Kung ang iyong dalawang kaibigan ay nag-sign ng iba pang mga sertipiko, pagkatapos ay maaari mong gamitin ang tiwala na mayroon ka sa iyong mga kaibigan upang tanggapin na ang ibang mga taong ito ay tunay na sinasabi nila na sila rin.

Ang mga kaibigan ng iyong mga kaibigan ay maaari nang pirmahan ang mga sertipiko ng mga taong pinagkakatiwalaan nila at iba pa, sa kalaunan ay nagtatayo ng isang malaking network ng mga indibidwal na pinagkakatiwalaan. Kapag ang mga webs ay makakakuha ng sapat na malaki at maging magkakaugnay sa iba pang mga web, maaari silang magamit bilang isang paraan upang mapagkakatiwalaan ang sinumang nasa network.

Ang higit pang mga lagda sa isang sertipiko, lalo na kung ang mga ito ay lagda mula sa lubos na pinagkakatiwalaang mga indibidwal, mas maaasahan mo ang digital na sertipiko ng isang tao at ang link sa pagitan ng kanilang pampublikong susi at kanilang pagkakakilanlan.

Ang mga gumagamit ng PGP ay madalas na humawak ng mga key party sa pag-sign kung saan magtipun-tipon ang mga tao upang mai-tsek ang kanilang mga pagkakakilanlan at nilagdaan ang kanilang mga digital na sertipiko. Ang mga pagtitipon na ito ay tumutulong upang magdala ng mga bagong tao sa network.

Bagaman kasama ito ng ilang mga pagiging kumplikado, ang bentahe ng sistema ng web ng tiwala ay walang gitnang katawan na maaaring masira.

Ligtas ba ang mga digital na lagda?

Sa isang pangkalahatang kahulugan, ang mga pirma sa digital ay ligtas maliban kung ang pribadong susi ng signee ay nakompromiso. Kung ang may-ari ay nagpapaalam sa ibang tao, iniwan ang pribadong susi na nakasulat, o nagnanakaw sa ibang paraan, kung gayon posible para sa isang umaatake na awtomatikong mag-sign ng mga mensahe na parang sila ang may-ari..

Ito ay maaaring humantong sa umaatake na nag-uugnay sa kanilang biktima o pag-aapi sa kanilang data. Ito ay isang malaking isyu sa seguridad, at ang sinumang naghihinala na ang kanilang susi ay nakompromiso ay dapat na bawiin ang kanilang digital na sertipiko na nag-uugnay sa kanila sa kanilang pampublikong susi, at magkaroon ng isang bagong inisyu..

Mayroong ilang iba pang mga caveats pagdating sa seguridad ng mga digital na lagda. Ang isang naaangkop na algorithm sa digital na lagda ay dapat gamitin, at kailangan din itong ipatupad nang maayos. Sa tabi nito, kailangan ding maging isang paraan ng pag-link sa pampublikong susi sa may-ari nito, karaniwang sa pamamagitan ng mga digital na sertipiko.

Hangga’t natutugunan ang mga kinakailangang ito, sumusunod ka sa pinakamahusay na kasanayan sa industriya, at ang iyong pribadong key ay hindi nakompromiso, kung gayon ang mga digital na lagda ay isang mahusay na paraan upang magbigay ng pagiging tunay, integridad at hindi pagtanggi sa data.

Nakabalangkas na Data ni Kai Stachowiak na lisensyado sa ilalim CC0