Ano ang RSA encryption at paano ito gumagana?
Ang RSA encryption ay isang system na malulutas kung ano ang dating isa sa mga pinakamalaking problema sa cryptography: Paano ka magpadala ng isang naka-code na mensahe nang walang pagkakaroon ng pagkakataon na maibahagi ang code sa kanila?
Ituturo sa iyo ng artikulong ito ang lahat ng kailangan mong malaman tungkol sa kung paano binuo ang pag-encrypt ng RSA, kung paano ito gumagana, ang matematika sa likod nito, kung ano ito ay ginagamit para sa pati na rin ang ilan sa mga pinakamalaking isyu sa seguridad na kinakaharap nito. Ang pag-aaral tungkol sa RSA ay magbibigay sa iyo ng ilang kaalaman sa kaalaman na makakatulong sa iyo upang maunawaan kung gaano karaming mga bahagi ng aming online na buhay ang pinananatiling ligtas.
Ano ang RSA encryption?
Sabihin nating nais mong sabihin sa iyong kaibigan ang isang lihim. Kung ikaw ay katabi ng mga ito, maaari mo lamang itong bulongin. Kung nasa tapat ka ng bansa, malinaw na hindi ito gagana. Maaari mong isulat ito at ipadala ito sa kanila, o gamitin ang telepono, ngunit ang bawat isa sa mga channel ng komunikasyon na ito ay hindi sigurado at ang sinumang may malakas na motibasyon ay madaling makagambala sa mensahe.
Kung ang lihim ay sapat na mahalaga, hindi mo ipagsapalaran ang pagsulat nito nang normal — ang mga tiktik o isang empleyado ng poste ng rogue ay maaaring tumingin sa iyong mail. Gayundin, ang isang tao ay maaaring i-tap ang iyong telepono nang walang iyong kaalaman at pag-log sa bawat solong tawag na iyong ginagawa.
Ang isang solusyon upang maiwasan ang mga eavesdropper na mai-access ang mga nilalaman ng mensahe ay i-encrypt ito. Ang pangunahing ito ay nangangahulugang magdagdag ng isang code sa mensahe na nagbabago nito sa isang gulo na gulo. Kung ang iyong code ay sapat na kumplikado, kung gayon ang tanging mga tao na makakapasok sa orihinal na mensahe ay ang mga may access sa code.
Kung nagkaroon ka ng pagkakataon na ibahagi ang code sa iyong kaibigan bago, kung gayon alinman sa iyo ay maaaring magpadala ng naka-encrypt na mensahe anumang oras, alam mong dalawa lang ang tanging may kakayahang basahin ang mga nilalaman ng mensahe. Ngunit paano kung wala kang pagkakataong ibahagi ang code nang una?
Ito ay isa sa mga pangunahing problema sa kriptograpiya, na tinalakay ng pampublikong-susi na mga scheme ng pag-encrypt (kilala rin bilang walang simetrya na pag-encrypt) tulad ng RSA.
Sa ilalim ng RSA encryption, ang mga mensahe ay naka-encrypt na may isang code na tinatawag na a pampublikong susi, na maibabahagi nang bukas. Dahil sa ilang natatanging mga katangian ng matematika ng algorithm ng RSA, sa sandaling naka-encrypt ang isang mensahe gamit ang pampublikong susi, maaari lamang itong mai-decry ng isa pang susi, na kilala bilang pribadong key. Ang bawat gumagamit ng RSA ay may pangunahing pares na binubuo ng kanilang pampubliko at pribadong mga susi. Tulad ng iminumungkahi ng pangalan, dapat itago ang pribadong key.
Iba’t ibang mga scheme ng pampublikong key encryption simetriko-key encryption, kung saan ang parehong proseso ng pag-encrypt at decryption ay gumagamit ng parehong pribadong key. Ang mga pagkakaiba-iba ay ginagawang pampublikong pangunahing pag-encrypt tulad ng RSA na kapaki-pakinabang para sa pakikipag-usap sa mga sitwasyon kung saan walang pagkakataon na ligtas na ipamahagi ang mga susi bago.
Ang mga etmmetric-key algorithm ay may sariling mga aplikasyon, tulad ng data ng pag-encrypt para sa personal na paggamit, o para sa kung may mga ligtas na mga channel na maibabahagi ang mga pribadong key.
Tingnan din: Public key kriptograpiya
Saan ginagamit ang pag-encrypt ng RSA?
Ang RSA encryption ay madalas na ginagamit sa pagsasama sa iba pang mga scheme ng pag-encrypt, o para sa mga pirma ng digital na maaaring patunayan ang pagiging tunay at integridad ng isang mensahe. Hindi karaniwang ginagamit ito upang i-encrypt ang buong mga mensahe o file, dahil ito ay hindi gaanong mahusay at mas mapagkukunan-mabigat kaysa sa simetriko-key encryption.
Upang maging mas mahusay ang mga bagay, sa isang file ay karaniwang mai-encrypt na may isang simetriko-key algorithm, at pagkatapos ay ang simetriko key ay mai-encrypt na may RSA encryption. Sa ilalim ng prosesong ito, ang isang entity lamang na may access sa RSA pribadong key ay magagawang i-decrypt ang simetriko key.
Nang hindi ma-access ang simetriko key, ang hindi mai-decrypted ang orihinal na file. Ang pamamaraang ito ay maaaring magamit upang mapanatiling ligtas ang mga mensahe at mga file, nang hindi kumukuha ng masyadong mahaba o ubusin ang napakaraming mapagkukunan ng computational.
Maaaring magamit ang pag-encrypt ng RSA sa isang iba’t ibang mga system. Maaari itong ipatupad sa OpenSSL, wolfCrypt, cryptlib at isang bilang ng iba pang mga aklatan ng cryptographic.
Bilang isa sa mga unang malawakang ginamit na mga scheme ng pag-encrypt ng publiko-key, inilatag ng RSA ang mga pundasyon para sa karamihan ng aming ligtas na komunikasyon. Ito ay ayon sa kaugalian na ginagamit sa TLS at din ang orihinal na algorithm na ginamit sa PGP encryption. Ang RSA ay nakikita pa rin sa isang saklaw ng mga web browser, email, VPN, chat at iba pang mga channel ng komunikasyon.
Madalas ding ginagamit ang RSA upang makagawa ng mga ligtas na koneksyon sa pagitan ng mga kliyente ng VPN at mga server ng VPN. Sa ilalim ng mga protocol tulad ng OpenVPN, maaaring magamit ng mga handshakes ng TLS ang algorithm ng RSA upang makipagpalitan ng mga susi at magtatag ng isang ligtas na channel.
Ang background ng RSA encryption
Tulad ng nabanggit namin sa simula ng artikulong ito, bago ang pag-encrypt ng publiko-key, isang hamon na makipag-usap nang ligtas kung hindi nagkaroon ng pagkakataon na ligtas na makipagpalitan ng mga susi bago. Kung walang pagkakataon na maibahagi ang code nang maaga, o isang ligtas na channel kung saan maipamahagi ang mga susi, walang paraan upang makipag-usap nang walang banta ng mga kaaway na makagambala at ma-access ang mga nilalaman ng mensahe.
Ito ay hindi hanggang sa 1970s na ang mga bagay ay talagang nagsimulang magbago. Ang unang pangunahing pag-unlad patungo sa tinatawag nating public-key na kriptograpiya ay nai-publish sa simula ng dekada ni James H. Ellis. Hindi makahanap si Ellis ng isang paraan upang maipatupad ang kanyang gawain, ngunit pinalawak ito ng kanyang kasamahan na si Clifford Cocks upang maging alam natin ngayon RSA encryption.
Ang pangwakas na piraso ng puzzle ay ang tinatawag natin ngayon Susi ng exchangeie-Hellman. Si Malcolm J. Williamson, isa pang katrabaho, ay gumawa ng isang pamamaraan na nagpapahintulot sa dalawang partido na magbahagi ng isang susi sa pag-encrypt, kahit na ang channel ay sinusubaybayan ng mga kalaban.
Ang lahat ng gawaing ito ay isinasagawa sa ahensya ng intelihensiya ng UK, ang Gobyerno ng Komunikasyon sa Gobyerno (GCHQ), na pinananatiling inuri ang pagtuklas. Bahagi dahil sa mga limitasyong teknolohikal, hindi nakikita ng GCHQ ang isang paggamit para sa public-key na kriptograpiya sa oras na iyon, kaya ang pag-unlad ay nakaupo lamang sa alikabok na nagtitipon ng alikabok. Ito ay hanggang sa 1997 na ang gawain ay idineklara at ang mga orihinal na imbentor ng RSA ay kinilala.
Makalipas ang ilang taon, ang mga katulad na konsepto ay nagsisimula na umunlad sa publiko. Ang Ralph Merkle ay lumikha ng isang maagang anyo ng pampublikong-susi kriptograpiya, na naimpluwensyahan sina Whitfield Diffie at Martin Hellman sa disenyo ng pagsasapalitan ng key key ng diffie-Hellman.
Ang mga ideya nina diffie at Hellman ay nawawala sa isang mahalagang aspeto na gagawing kanilang gawain bilang pundasyon ng pampublikong pangunahing krokograpiya. Ito ay isang one-way function na magiging mahirap baligtarin. Noong 1977, Ron Rivest, Adi Shamir at Leonard Adleman, na ang mga huling pangalan ay bumubuo ng acronym RSA, ay dumating sa isang solusyon pagkatapos ng isang taon ng pagtatrabaho sa problema.
Ang akademikong nakabase sa MIT ay gumawa ng kanilang pagtatapos matapos ang isang pagdiriwang ng Paskuwa noong 1977. Matapos ang isang gabi ng pag-inom, umuwi si Rivest, ngunit sa halip na matulog, ginugol niya ang gabing nag-aalalang sumulat ng isang papel na nagpormal ng kanyang ideya para sa kinakailangang pag-andar na one-way.
Ang ideya ay patentado sa 1983 ng MIT, ngunit hindi hanggang sa mga unang araw ng internet na ang RSA algorithm ay nagsimulang makita ang laganap na pag-ampon bilang isang mahalagang kasangkapan sa seguridad.
Paano gumagana ang pag-encrypt ng RSA?
Ang mga sumusunod ay magiging isang maliit na kadali, sapagkat napakaraming mga mambabasa na marahil ay na-scarred ng kanilang guro sa matematika sa high school. Upang mapanatili ang matematika sa pagkuha ng masyadong out-of-hand, magiging kami pagpapagaan ng ilang mga konsepto at paggamit ng mas maliit na mga numero. Sa katotohanan, ang pag-encrypt ng RSA ay gumagamit ng mga pangunahing numero na mas malaki sa kalakhan at mayroong ilang iba pang mga pagiging kumplikado.
Mayroong maraming mga magkakaibang mga konsepto na kakailanganin mong mapunta ang iyong ulo bago namin maipaliwanag kung paano magkasama ang lahat. Kabilang dito mga pag-andar sa trapiko, pagbuo ng primes, ganap na pagpapaandar ng Carmichael at ang mga hiwalay na proseso na kasangkot pag-compute ng pampubliko at pribadong mga susi ginamit sa mga proseso ng pag-encrypt at decryption.
Mga function ng trap ng pinto
Ang RSA encryption ay gumagana sa ilalim ng saligan na ang algorithm ay madaling makalkula sa isang direksyon, ngunit halos imposible sa baligtad. Bilang halimbawa, kung sinabihan ka na ang 701,111 ay isang produkto ng dalawang pangunahing numero, malalaman mo ba kung ano ang dalawang numero na iyon?
Kahit na sa isang calculator o isang computer, ang karamihan sa atin ay walang ideya kung saan magsisimula, hayaan mong malaman ang sagot. Ngunit kung i-flip namin ang mga bagay sa paligid, nagiging mas madali ito. Ano ang resulta ng:
907 x 773
Kung naiinip ka na, magagawa mong masusuka ang iyong telepono o marahil makalkula ito sa iyong ulo upang malaman na ang sagot ay ang naunang nabanggit 701,111. Ang 907 at 773 na ito ang mga pangunahing numero na sumasagot sa aming unang katanungan, na nagpapakita sa amin na ang ilang mga equation ay maaaring madaling malaman ang isang paraan, ngunit tila imposible sa baligtad.
Ang isa pang kawili-wiling aspeto ng ekwasyong ito ay simple upang malaman ang isa sa mga pangunahing numero kung mayroon ka pang iba, pati na rin ang produkto. Kung sinabihan ka na ang 701,111 ay ang resulta ng 907 na pinarami ng isa pang kalakhang numero, maaari mong malaman ito sa iba pang punong may sumusunod na equation:
701,111 ÷ 907 = 773
Dahil ang ugnayan sa pagitan ng mga bilang na ito ay simple upang makalkula sa isang direksyon, ngunit hindi mapaniniwalaan o kapani-paniwala mahirap sa kabaligtaran, ang equation ay kilala bilang isang pag-andar ng pinto ng bitag. Maging kamalayan na habang ang halimbawa sa itaas ay mahirap para sa mga tao na malaman, ang mga computer ay maaaring gawin ang operasyon sa isang walang halaga na oras.
Dahil dito, ang RSA ay gumagamit ng mas malaking bilang. Ang laki ng mga prima sa isang tunay na pagpapatupad ng RSA ay nag-iiba, ngunit sa 2048-bit na RSA, magkasama silang magsasagawa ng mga susi na haba ng 617 na numero. Upang matulungan kang mailarawan ito, ang isang susi ay magiging isang bilang ng sukat na ito:
99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999
Bumubuo ng mga primes
Ang mga pag-andar ng pinto ng bitag na nabanggit sa itaas ay bumubuo ng batayan para sa kung paano gumagana ang pampubliko at pribadong-key na mga scheme ng pag-encrypt. Pinapayagan ng kanilang mga pag-aari ang mga pampublikong susi upang maibahagi nang walang panganib sa mensahe o ibubunyag ang pribadong key. Pinapayagan din nila ang data na mai-encrypt gamit ang isang key sa isang paraan na maaari lamang mai-decry ng iba pang susi mula sa pares.
Ang unang hakbang ng pag-encrypt ng isang mensahe kasama ang RSA ay makabuo ng mga susi. Upang gawin ito, kailangan namin dalawang pangunahing numero (p at q) na napili gamit ang isang pagsubok sa primidad. Ang isang pagsubok sa primidad ay isang algorithm na mahusay na nakakahanap ng mga pangunahing numero, tulad ng pagsubok sa primity ng Rabin-Miller.
Ang mga pangunahing numero sa RSA ay kailangang maging napakalaki, at medyo malayo rin ang hiwalay. Ang mga numero na maliit o mas malapit nang magkasama ay mas madaling mag-crack. Sa kabila nito, gagamitin ng aming halimbawa ang mas maliit na mga numero upang gawing mas madaling sundin at makalkula ang mga bagay.
Sabihin natin na ang primity test ay nagbibigay sa amin ng mga pangunahing numero na ginamit namin sa itaas, 907 at 773. Ang susunod na hakbang ay upang matuklasan ang modulus (n), gamit ang sumusunod na formula:
n = p x q
Saan p = 907 at q = 773
Samakatuwid:
n = 907 x 773
n = 701,111
Ang buong pag-andar ni Carmichael
Sa sandaling mayroon kami n, ginagamit namin Ang buong pag-andar ni Carmichael:
λ(n) = lcm (p – 1, q – 1)
Kung matagal-tagal na mula nang na-hit mo ang mga aklat-aralin sa matematika, maaaring mukhang nakakatakot ang nasa itaas. Maaari mong laktawan ang bahaging ito at tiwala lamang na gumagana ang matematika, kung hindi man ay manatili sa amin para sa ilang higit pang mga kalkulasyon. Ang lahat ay ipapaliwanag sa mas maraming detalye hangga’t maaari upang matulungan kang mapunta ang iyong ulo sa paligid ng mga pangunahing kaalaman.
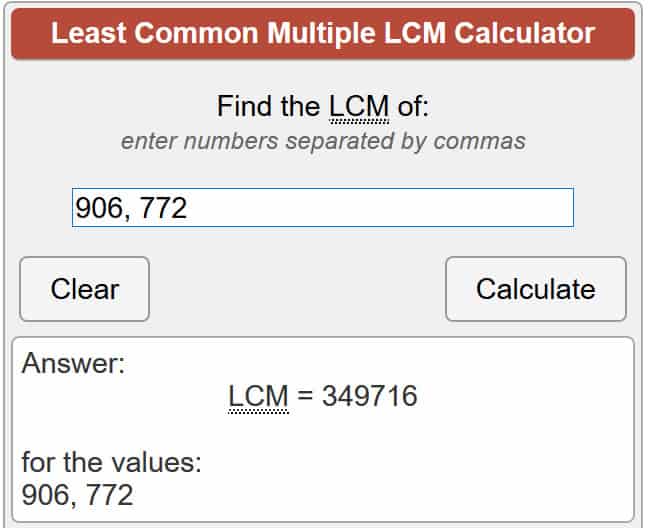
Para sa mga hindi nakakaalam, λ (n) kumakatawan sa Carmichael para sa n, habang lcm nangangahulugang pinakamababang karaniwang maramihang, na siyang pinakamababang bilang na pareho p at q maaaring hatiin sa. Mayroong ilang iba’t ibang mga paraan upang malaman ito, ngunit ang pinakamadali ay ang pagtitiwala sa isang online calculator na gawin ang equation para sa iyo. Kaya ilagay ang aming mga numero sa equation:
λ(701,111) = lcm (907 – 1, 773 – 1)
λ(701,111) = lcm (906, 772)
Gamit ang naka-link sa calculator sa itaas, nagbibigay ito sa amin:
λ(701,111) = 349,716
Bumubuo ng susi ng publiko
Ngayon na mayroon kami ng Carmichael ng kabuuan ng aming mga pangunahing numero, ito ay oras upang malaman ang aming pampublikong susi. Sa ilalim ng RSA, ang mga pampublikong susi ay binubuo ng isang pangunahing numero e, pati na rin ang n. Ang numero e maaaring maging anumang bagay sa pagitan ng 1 at ang halaga para sa λ(n), na sa aming halimbawa ay 349,716.
Dahil ang pampublikong susi ay bukas na ibinahagi, hindi ito mahalaga para sa e upang maging isang random na numero. Sa pagsasagawa, e sa pangkalahatan ay nakatakda sa 65,537, dahil kapag ang mas malaking mga numero ay pinili nang sapalaran, ginagawang mas mahusay ang pag-encrypt. Para sa halimbawa ngayon, panatilihin naming maliit ang mga numero upang maging mahusay ang mga kalkulasyon. Sabihin nating:
e = 11
Ang aming panghuling naka-encrypt na data ay tinatawag na ciphertext (c). Nakukuha namin ito mula sa aming plaintext message (m), sa pamamagitan ng paglalapat ng pampublikong susi gamit ang sumusunod na pormula:
c = me mod n
Naabutan na namin e at alam natin n din. Ang kailangan lang nating ipaliwanag ay mod. Medyo wala sa kalaliman ng artikulong ito, ngunit tumutukoy ito sa isang operasyon ng modulo, na nangangahulugang nangangahulugan na ang nalalabi ay natitira kapag hatiin mo ang isang panig sa kabilang linya. Halimbawa:
10 mod 3 = 1
Ito ay dahil ang 3 ay pumapasok sa 10 tatlong beses, na may natitira sa 1.
Bumalik sa aming equation. Upang panatilihing simple ang mga bagay, sabihin iyan ang mensahe (m) na nais nating i-encrypt at panatilihing lihim ay iisa lamang ang bilang, 4. I-plug ang lahat sa:
c = me mod n
c = 411 mod 701,111
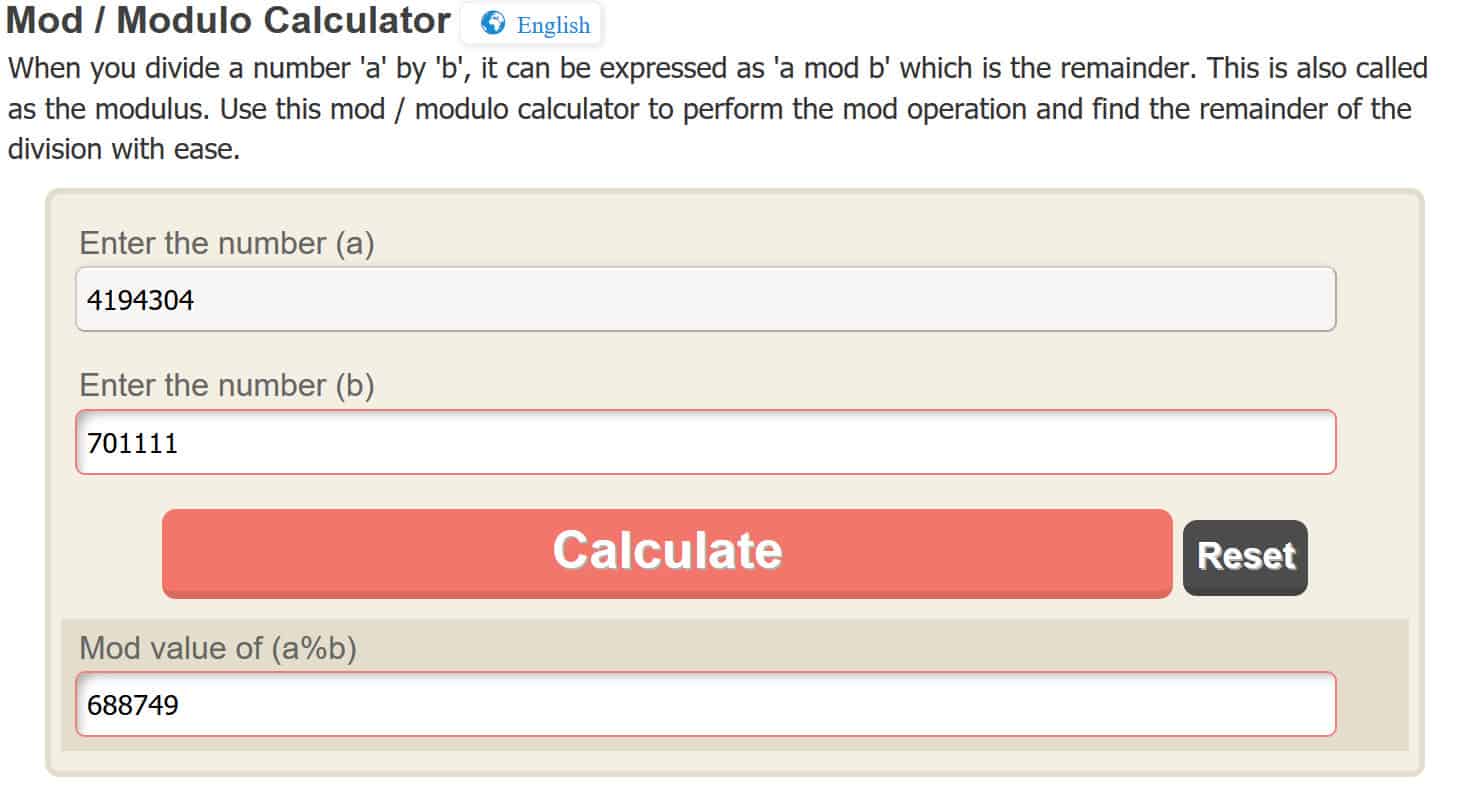
c = 4,194,304 mod 701,111
Muli, upang gawin ang operasyon ng modulo madali, gumagamit kami ng isang online calculator, ngunit malugod mong malaman ito para sa iyong sarili. Sa pamamagitan ng pagpasok ng 4,194,304 sa online calculator, binibigyan kami nito:
c = 688,749
Samakatuwid kapag ginagamit namin ang RSA upang i-encrypt ang aming mensahe, 4, sa aming pampublikong susi, binibigyan tayo nito ciphertext ng 688,749. Ang mga nakaraang hakbang ay maaaring tila medyo mabigat sa matematika, ngunit mahalaga na muling isulat kung ano ang tunay na nangyari.
Nagkaroon kami ng isang mensahe ng 4, na nais naming itago ang lihim. Nag-apply kami ng isang pampublikong susi dito, na nagbigay sa amin ng naka-encrypt na resulta ng 688,749. Ngayon na ito ay naka-encrypt, ligtas naming maipadala ang numero 688,749 sa may-ari ng pangunahing pares. Ang mga ito lamang ang taong makakapag-decry ng mga ito gamit ang kanilang pribadong susi. Kapag nai-decrypt nila ito, makikita nila ang mensahe na talagang ipinadala namin, 4.
Bumubuo ng pribadong susi
Sa pag-encrypt ng RSA, sa sandaling ang data o isang mensahe ay naging ciphertext na may pampublikong susi, maaari lamang itong mai-decry ng pribadong susi mula sa parehong key na pares. Ang mga pribadong key ay binubuo ng d at n. Alam na natin n, at ang sumusunod na equation ay ginagamit upang hanapin d:
d = 1 /e mod λ(n)
Nasa Bumubuo ng susi ng publiko seksyon sa itaas, napagpasyahan na namin na sa aming halimbawa, e ay pantay na 11. Gayundin, alam natin na λ(n) katumbas ng 349,716 mula sa aming mas maagang gawain sa ilalim Ang buong pag-andar ni Carmichael. Ang mga bagay ay nakakakuha ng isang maliit na mas kumplikado kapag natagpuan namin ang seksyon na ito ng pormula:
1 /e mod
Ang ekwasyong ito ay maaaring magmukhang hinihiling sa iyo na hatiin ang 1 hanggang 11, ngunit hindi iyon ang nangyari. Sa halip, ito ay sumisimbolo lamang na kailangan nating kalkulahin ang modular na kabaligtaran ng e (na sa kasong ito ay 11) at λ(n) (na sa kasong ito ay 349,716).
Ito ay nangangahulugang nangangahulugan na sa halip na magsagawa ng isang karaniwang operasyon ng modulo, gagamitin namin ang kabaligtaran. Karaniwang matatagpuan ito sa Extended Euclidean Algorithm, ngunit kaunti ito sa labas ng saklaw ng artikulong ito, kaya gagawa lang kami at gagamitin ang isang online calculator. Ngayon naiintindihan namin ang lahat ng nangyayari, hayaan ang plug ng aming impormasyon sa pormula:
d = 1 /11 mod 349,716
Upang maisagawa ang operasyon na ito, i-input lamang ang 11 (o anumang halaga na maaaring mayroon ka para sa e kung sinusubukan mo ito sa iyong sariling halimbawa) kung saan sinasabi nito Integer at 349,716 (o anumang halaga na maaaring mayroon ka para sa λ(n) kung sinusubukan mo ito sa iyong sariling halimbawa) kung saan sinasabi nito Modulo sa online calculator na naka-link sa itaas. Kung ginawa mo ito nang tama, dapat kang makakuha ng isang resulta kung saan:
d = 254, 339
Ngayon mayroon tayong halaga para sa d, maaari naming i-decrypt ang mga mensahe na naka-encrypt sa aming pampublikong susi gamit ang sumusunod na pormula:
m = cd mod n
Maaari na kaming bumalik sa ciphertext na naka-encrypt sa ilalim ng Bumubuo ng pribadong susi seksyon. Kapag na-encrypt namin ang mensahe gamit ang pampublikong susi, binigyan kami ng isang halaga para sa c ng 688,749. Mula sa itaas, alam natin iyon d katumbas ng 254,339. Alam din natin yun n katumbas ng 701,111. Nagbibigay ito sa amin:
m = 688,749254,339 mod 701,111.
Tulad ng napansin mo, ang pagsisikap na kumuha ng isang numero sa 254,339 na kapangyarihan ay maaaring medyo kaunti para sa karamihan sa mga normal na calculator. Sa halip, gumagamit kami ng isang online RSA decryption calculator. Kung nais mong gumamit ng isa pang pamamaraan, ilalapat mo ang mga kapangyarihan tulad ng karaniwan mong gagawin at isinasagawa ang modulus operation sa parehong paraan tulad ng ginawa namin sa Bumubuo ng susi ng publiko seksyon.
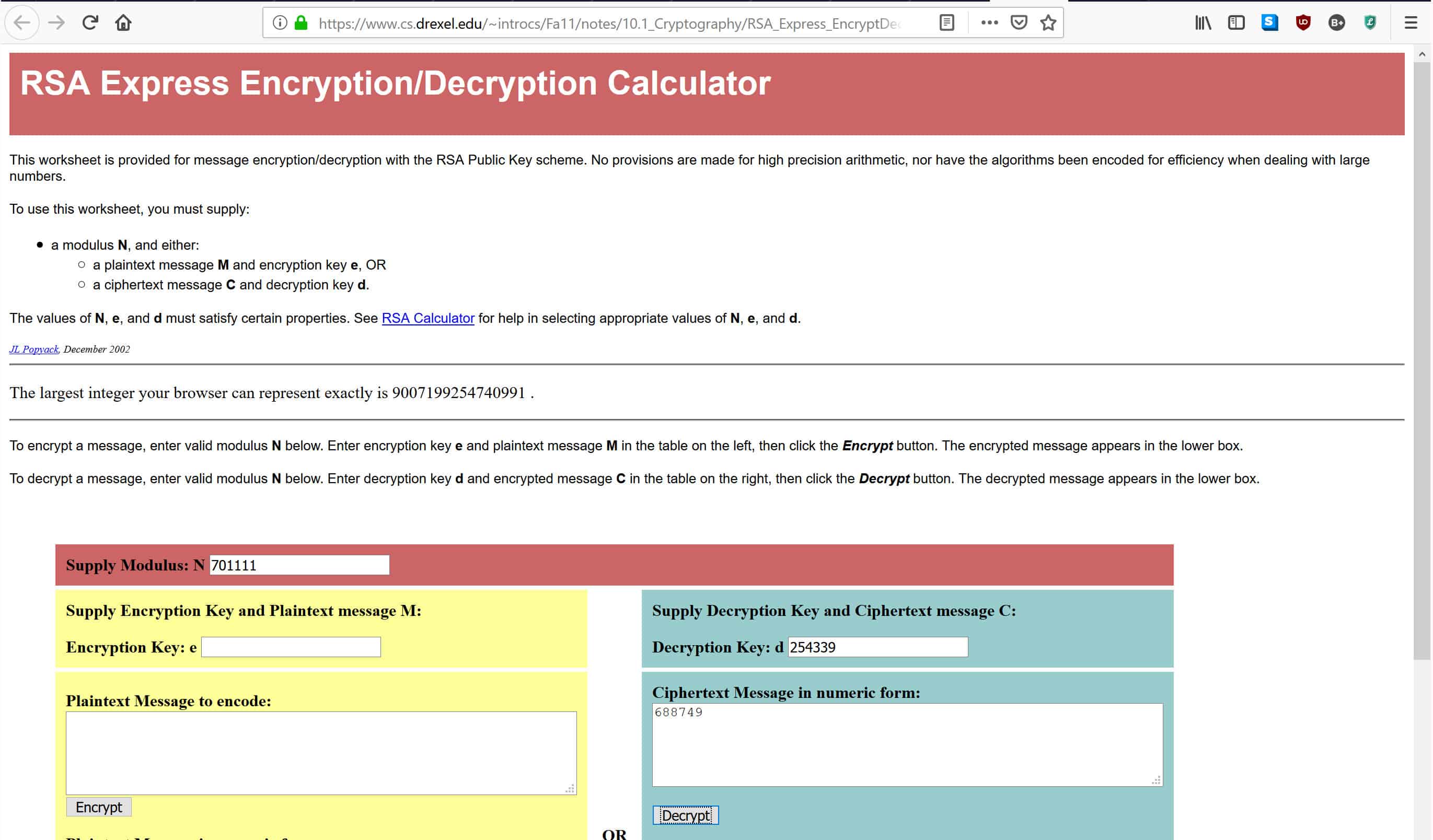
Sa calculator na naka-link sa itaas, ipasok ang 701,111 kung saan sinasabi nito Pagbibigay ng Modulus: N, 254,399 kung saan sinasabi nito Susi ng decryption: D, at 688,749 kung saan sinasabi nito Ciphertext na Mensahe sa numerong form, tulad ng ipinakita sa ibaba:
Kapag naipasok mo ang data, pindutin I-decrypt, na mailalagay ang mga numero sa pamamagitan ng formula ng decryption na nakalista sa itaas. Bibigyan ka nito ng orihinal na mensahe sa kahon sa ibaba. Kung nagawa mo nang tama ang lahat, dapat kang makakuha ng sagot ng 4, na siyang orihinal na mensahe na na-encrypt namin sa aming pampublikong susi.
Paano gumagana ang pag-encrypt ng RSA sa pagsasanay
Ang mga seksyon sa itaas ay dapat magbigay sa iyo ng isang makatwirang pag-uunawa kung paano gumagana ang matematika sa likod ng pampublikong key key encryption. Maaari itong maging isang maliit na nakalilito, ngunit kahit na ang mga hindi maintindihan ang mga pagkasalimuot ng mga equation ay maaaring umaalis sa ilang mahalagang impormasyon tungkol sa proseso.
Sa mga hakbang na nakalista sa itaas, ipinakita namin kung paano ligtas na makipag-usap ang dalawang mga nilalang nang hindi na nagbahagi ng dati nang code. Una, kailangan nila ng bawat isa set up ng kanilang sariling mga key pares at ibahagi ang pampublikong susi sa isa’t isa. Ang dalawang entidad ay kailangang panatilihing lihim ang kanilang mga pribadong key upang ang kanilang mga komunikasyon ay mananatiling ligtas.
Kapag ang nagpadala ay may pampublikong susi ng kanilang tatanggap, maaari nilang gamitin ito upang i-encrypt ang data na nais nilang mapanatili ang ligtas. Kapag na-encrypt na ito gamit ang isang pampublikong susi, maaari lamang itong mai-decry ng pribadong key mula sa parehong key na pares. Kahit na ang parehong pampublikong key ay hindi magamit upang i-decrypt ang data. Ito ay dahil sa mga katangian ng mga pag-andar ng pinto ng trap na nabanggit natin sa itaas.
Kapag natanggap ng tatanggap ang naka-encrypt na mensahe, ginagamit nila ang kanilang pribadong key upang ma-access ang data. Kung ang tatanggap ay nais na ibalik ang mga komunikasyon sa isang ligtas na paraan, maaari nilang mai-encrypt ang kanilang mensahe sa pampublikong susi ng partido na kanilang nakikipag-usap. Muli, sa sandaling nai-encrypt na ito sa pampublikong susi, ang tanging paraan na ma-access ang impormasyon ay sa pamamagitan ng pagtutugma ng pribadong key.
Sa ganitong paraan, ang pag-encrypt ng RSA ay maaaring magamit ng mga dating hindi kilalang partido upang ligtas na magpadala ng data sa pagitan ng kanilang sarili. Ang mga makabuluhang bahagi ng mga channel ng komunikasyon na ginagamit namin sa aming online na buhay ay binuo mula sa pundasyong ito.
Paano naka-encrypt ang mga mas kumplikadong mensahe sa RSA?
Sa aming halimbawa, pinasimple namin ang mga bagay upang mas madaling maunawaan, na ang dahilan kung bakit naka-encrypt lamang kami ng isang mensahe ng “4”. Ang kakayahang i-encrypt ang numero 4 ay tila hindi kapaki-pakinabang, kaya maaari kang magtataka kung paano mo mai-encrypt ang isang mas kumplikadong hanay ng data, tulad ng isang simetriko key (na kung saan ay ang pinaka-karaniwang paggamit ng RSA), o kahit isang mensahe.
Ang ilang mga tao ay maaaring magulo sa kung paano ang isang key tulad ng “n38cb29fkbjh138g7fqijnf3kaj84f8b9f …” o isang mensahe tulad ng “bumili ako ng sandwich” ay maaaring mai-encrypt ng isang algorithm tulad ng RSA, na tumutukoy sa mga numero at hindi mga titik. Ang katotohanan ay ang lahat ng impormasyon na ang proseso ng aming computer ay naka-imbak sa binary (1s at 0s) at gumagamit kami ng mga pamantayan sa pag-encode tulad ng ASCII o Unicode upang kumatawan sa kanila sa mga paraan na maiintindihan ng tao (mga titik).
Nangangahulugan ito na ang mga susi tulad ng “n38cb29fkbjh138g7fqijnf3kaj84f8b9f …” at mga mensahe tulad ng “bumili ako ng sandwich” na mayroon nang bilang mga numero, na madaling makalkula sa algorithm ng RSA. Ang mga bilang na kinakatawan ng mga ito ay mas malaki at mahirap para sa amin upang pamahalaan, na kung bakit mas gusto naming makitungo sa mga character na alphanumeric sa halip na isang pagbagsak ng binary.
Kung nais mo i-encrypt ang isang mas mahahalagang session key o isang mas kumplikadong mensahe sa RSA, nais lamang itong kasangkot sa mas malaking bilang.
Padding
Kapag ipinatupad ang RSA, gumagamit ito ng isang bagay na tinatawag padding upang makatulong na maiwasan ang isang bilang ng mga pag-atake. Upang ipaliwanag kung paano ito gumagana, magsisimula tayo sa isang halimbawa. Sabihin nating nagpadala ka ng isang naka-code na mensahe sa isang kaibigan:
Mahal na Karen,
Sana maayos ka. Maghanda pa ba tayo bukas?
Taimtim na,
James
Sabihin nating na iyong nai-code ang mensahe sa isang simpleng paraan, sa pamamagitan ng pagbabago ng bawat titik sa isa na sumusunod sa alpabeto. Magbabago ito ng mensahe sa:
Efbs Lbsfo,
J ipqf zpv bsf xfmm. Bsf xf tujmm ibwjoh ejoofs upnpsspx?
Zpvst tjodfsfmz,
Kbnft
Kung naharang ng iyong mga kaaway ang liham na ito, mayroong isang trick na maaari nilang gamitin upang subukan at basag ang code. Kaya nila tingnan ang format ng iyong liham at subukang hulaan kung ano ang maaaring sabihin ng mensahe. Alam nila na ang mga tao ay karaniwang nagsisimula ng kanilang mga titik na may “Kumusta”, “Kumusta”, “Mahal” o maraming iba pang mga kombensyon.
Kung sinubukan nilang ilapat ang “Kumusta” o “Kumusta” bilang unang salita, makikita nila na hindi ito akma sa bilang ng mga character. Pagkatapos ay maaari nilang subukan ang “Mahal”. Nababagay ito, ngunit hindi iyon nangangahulugang anumang bagay. Susubukan lang ito ng mga sumasalakay at makita kung saan pinangunahan sila. Kaya ibabago nila ang mga titik na “e”, “f”, “b”, at “s” na may “d”, “e”, “a”, at “r” ayon sa pagkakabanggit. Ito ang magbibigay sa kanila:
Mahal na Laseo,
J ipqe zpv ay xemm. Sigurado xe tujmm iawjoh djooes upnpsspx?
Zpvrt tjoderemz,
Kanet
Mukha pa ring nakakalito, kaya maaaring subukan ng mga umaatake ang ilang iba pang mga kombensiyon, tulad ng kung paano namin tapusin ang aming mga titik. Ang mga tao ay madalas na nagdaragdag ng “Mula” o “Magandang regards” sa dulo, ngunit alinman sa mga ito ay hindi angkop sa format. Sa halip, maaaring subukan ng mga umaatake ang “Kayo nang taimtim” at palitan ang iba pang mga titik upang makita kung saan ito nakuha. Sa pamamagitan ng pagpapalit ng “z”, “p”, “v”, “t”, “j” “o”, “d” at “m” ng “y”, “o”, “u”, “s”, ” ako “,” n “,” c “at” l “ayon sa pagkakabanggit, makakakuha sila:
Mahal na Lasen,
Akoqe ikaw ay xell. Sigurado xe tuill iawinh dinnes uonossox?
Taimtim na,
Kanet
Matapos ang modipikasyong iyon, mukhang nagsisimula ang pagkuha ng mga umaatake. Natagpuan nila ang mga salitang “Ako”, “ikaw” at “ay”, bilang karagdagan sa mga salitang binubuo ng kanilang mga unang hula.
Nakakakita na ang mga salita ay nasa wastong pagkakasunud-sunod ng gramatika, ang mga umaatake ay maaaring maging kumpiyansa na sila ay papunta sa tamang direksyon. Sa ngayon, natanto din nila na ang code ay kasangkot ang bawat titik na binago sa isa na sumusunod sa alpabeto. Sa sandaling napagtanto ito, ginagawang madali itong isalin ang natitira at basahin ang orihinal na mensahe.
Ang halimbawa sa itaas ay isang simpleng code, ngunit tulad ng nakikita mo, ang istraktura ng isang mensahe ay maaaring magbigay ng mga pahiwatig sa mga umaatake tungkol sa nilalaman nito. Sigurado, mahirap malaman ang mensahe mula lamang sa istraktura nito at kinuha ang ilang pinag-aralan na hula, ngunit kailangan mong tandaan na ang mga computer ay mas mahusay sa paggawa nito kaysa sa kami. Nangangahulugan ito na maaari silang magamit upang malaman ang mas kumplikadong mga code sa mas mas maikling oras, batay sa mga pahiwatig na nagmula sa istraktura at iba pang mga elemento.
Kung ang istraktura ay maaaring humantong sa isang code na basag at ibunyag ang mga nilalaman ng isang mensahe, kailangan namin ng ilang paraan upang maitago ang istraktura upang mapanatili ang ligtas na mensahe. Dinadala tayo nito padding.
Kapag may mensahe na naka-pad, ang randomized data ay idinagdag upang itago ang orihinal na mga pahiwatig ng pag-format na maaaring humantong sa isang naka-encrypt na mensahe na nasira. Sa RSA, ang mga bagay ay medyo mas kumplikado, dahil ang isang naka-encrypt na susi ay walang malinaw na pag-format ng isang liham na nakatulong upang bigyan kami ng mga pahiwatig sa aming halimbawa sa itaas.
Sa kabila nito, ang mga kaaway ay maaaring gumamit ng maraming mga pag-atake upang samantalahin ang mga katangian ng matematika ng isang code at masira ang naka-encrypt na data. Dahil sa banta na ito, pagpapatupad ng RSA gamitin ang mga padding scheme tulad ng OAEP upang mag-embed ng dagdag na data sa mensahe. Ang pagdaragdag ng padding na ito bago mai-encrypt ang mensahe ay ginagawang mas ligtas ang RSA.
Pag-sign ng mga mensahe
Ang RSA ay maaaring magamit para sa higit pa sa naka-encrypt na data. Ginagawa din nito ang isang kapaki-pakinabang na sistema para sa Kinumpirma na ang isang mensahe ay ipinadala ng entidad na nagsasabing nagpadala nito, pati na rin ang pagpapatunay na ang isang mensahe ay hindi binago o pinalit ng.
Kapag nais ng isang tao na patunayan ang pagiging tunay ng kanilang mensahe, maaari silang makalkula a hash (isang function na tumatagal ng data ng isang di-makatarungang laki at lumiliko ito sa isang nakapirming haba na halaga) ng plaintext, pagkatapos ay pirmahan ito sa kanilang pribadong key. Sila lagdaan ang hash sa pamamagitan ng paglalapat ng parehong formula na ginagamit sa decryption (m = cd mod n). Kapag naka-sign ang mensahe, ipinadala nila ang digital na pirma na ito sa tatanggap kasama ang mensahe.
Kung ang isang tatanggap ay tumatanggap ng isang mensahe gamit ang isang digital na lagda, maaari nilang gamitin ang lagda upang suriin kung ang mensahe ay tunay na nilagdaan ng pribadong susi ng taong sinasabing nagpadala nito. Maaari rin nilang makita kung ang mensahe ay nabago ng mga umaatake matapos itong maipadala.
Upang suriin ang digital na lagda, ang tatanggap ay unang gumamit ng parehong function ng hash upang mahanap ang hash na halaga ng mensahe na kanilang natanggap. Ang tatanggap pagkatapos ay inilalapat ang pampublikong susi ng nagpadala sa digital na lagda, gamit ang formula ng pag-encrypt (c = me mod n), upang bigyan sila ng abala ng digital na lagda.
Ni paghahambing ng hadh ng mensahe na natanggap sa tabi ng hash mula sa naka-encrypt na digital na lagda, ang tatanggap ay maaaring sabihin kung ang mensahe ay tunay. Kung ang parehong mga halaga ay pareho, ang mensahe ay hindi nabago mula nang pumirma ng orihinal na nagpadala. Kung ang mensahe ay binago ng kahit isang solong character, ang halaga ng hash ay magiging ganap na magkakaiba.
Seguridad ng RSA & pag-atake
Tulad ng karamihan sa mga cryptosystem, ang seguridad ng RSA ay depende sa kung paano ito ipinatupad at ginagamit. Ang isang mahalagang kadahilanan ay ang laki ng susi. Ang mas malaki ang bilang ng mga piraso sa isang susi (mahalagang kung gaano katagal ang susi), mas mahirap na masira ang mga pag-atake tulad ng brute-forcing at factoring.
Dahil ang mga asymmetric-key algorithm tulad ng RSA ay maaaring masira ng integer factorization, habang ang simetriko-key algorithm tulad ng AES ay hindi, ang mga pindutan ng RSA ay kailangang mas mahaba upang makamit ang parehong antas ng seguridad.
Sa kasalukuyan, ang pinakamalaking pinakamalaking sukat na na-factored ay 768 bits ang haba. Ginawa ito ng isang koponan ng akademya sa loob ng isang dalawang taon, gamit ang daan-daang mga makina.
Dahil ang pagkumpleto ay nakumpleto sa pagtatapos ng 2009 at ang kapangyarihan ng computing ay lumago nang malaki mula noong panahong iyon, maaari itong ipagpalagay na isang pagtatangka ng katulad na intensity maaari na ngayong salikin ang isang mas malaking RSA key.
Sa kabila nito, ang oras at mga mapagkukunan na kinakailangan para sa ganitong uri ng pag-atake ay inilalampasan nito ang karamihan sa mga hacker at sa lupain ng mga estado ng bansa. Ang pinakamahusay na haba ng susi na gagamitin ay depende sa iyong indibidwal na modelo ng banta. Ang National Institute of Standards and Technology Inirerekomenda ang isang minimum na sukat ng sukat ng 2048-bit, ngunit ang 4096-bit key ay ginagamit din sa ilang mga sitwasyon kung saan mas mataas ang antas ng pagbabanta.
Ang Factoring ay isang paraan lamang na maaaring masira ang RSA. Ang isang bilang ng iba pang mga pag-atake ay may potensyal na masira ang pag-encrypt na may mas maliit na halaga ng mga mapagkukunan, ngunit ang mga ito ay nakasalalay sa pagpapatupad at iba pang mga kadahilanan, hindi kinakailangan mismo ang RSA. Ang ilan sa mga ito ay kinabibilangan ng:
Random ba talaga ang primes?
Ang ilang mga pagpapatupad ng RSA ay gumagamit ng mahina na random number generators upang makabuo ng mga primes. Kung ang mga numerong ito ay hindi sapat na random, ginagawang mas madali para sa mga umaatake na salikin ang mga ito at masira ang pag-encrypt. Itong problema maiiwasan sa pamamagitan ng paggamit ng isang cryptograpically secure na pseudo-random number generator.
Mahina key generation
Ang mga key ng RSA ay kailangang mahulog sa loob ng ilang mga parameter upang sila ay maging ligtas. Kung ang primes p at q ay masyadong malapit na magkasama, ang susi ay madaling matuklasan. Gayundin, ang bilang d na binubuo ng bahagi ng pribadong key ay hindi maaaring maliit. Ang isang mababang halaga ay ginagawang madali upang malutas. Mahalaga na ang mga numerong ito ay may sapat na haba upang mapanatiling ligtas ang iyong susi.
Pag-atake sa gilid ng channel
Ito ay isang uri ng pag-atake na hindi masira ang RSA nang direkta, ngunit sa halip ay gumamit ng impormasyon mula sa pagpapatupad nito upang magbigay ng mga pahiwatig sa mga umaatake tungkol sa proseso ng pag-encrypt. Ang mga pag-atake na ito ay maaaring magsama ng mga bagay tulad pag-aaral sa dami ng kapangyarihan na ginagamit, o pagtatasa ng hula sa sangay, na gumagamit ng mga sukat sa pagpapatupad ng oras upang matuklasan ang pribadong susi.
Ang isa pang uri ng pag-atake sa gilid ng channel ay kilala bilang isang pag-atake sa tiyempo. Kung ang isang nagsasalakay ay may kakayahang masukat ang oras ng pag-decryption sa computer ng kanilang target para sa maraming iba’t ibang mga naka-encrypt na mensahe, ang impormasyong ito ay posible para sa umaatake upang alamin ang pribadong susi ng target.
Karamihan sa mga pagpapatupad ng RSA ay maiwasan ang pag-atake na ito sa pamamagitan ng pagdaragdag ng isang one-off na halaga sa panahon ng proseso ng pag-encrypt, na nag-aalis ng ugnayan na ito. Ang prosesong ito ay tinatawag blindographic blinding.
Ligtas ba ang pag-encrypt ng RSA para sa hinaharap?
Ang mabuting balita ay ang RSA ay itinuturing na ligtas na gagamitin, sa kabila ng mga posibleng pag-atake na ito. Ang caveat na yan kailangang maipatupad nang tama at gumamit ng isang susi na nahuhulog sa loob ng tamang mga parameter. Tulad ng napag-usapan na natin, ang mga pagpapatupad na hindi gumagamit ng padding, gumamit ng hindi sapat na sukat ng mga prima o may iba pang mga kahinaan ay hindi maaaring ituring na ligtas.
Kung nais mong gumamit ng RSA encryption, tiyaking gumagamit ka ng susi ng hindi bababa sa 1024 bit. Ang mga may mas mataas na modelo ng banta ay dapat manatili sa mga susi ng 2048 o 4096 na piraso kung nais nilang gamitin ang RSA nang may kumpiyansa. Hangga’t alam mo ang mga kahinaan na mayroon at ginamit ito ng RSA, dapat mong pakiramdam na ligtas na gamitin ang RSA para sa key pagbabahagi at iba pang katulad na mga gawain na nangangailangan ng pampublikong key encryption.
Tingnan din: Ipinaliwanag ang mga karaniwang uri ng pag-encrypt