Що таке шифрування RSA і як це працює?
Шифрування RSA – це система, яка вирішує те, що колись було однією з найбільших проблем криптографії: Як можна надіслати комусь кодоване повідомлення не маючи можливості попередньо ділитися з ними кодом?
Ця стаття навчить вас усьому, що вам потрібно знати як було розроблено шифрування RSA, як це працює, математика за нею, для чого він використовується а також деякі з найбільші проблеми безпеки, з якими стикаються. Дізнавшись про RSA, ви дасте кілька фундаментальних знань, які допоможуть вам зрозуміти, скільки частин нашого життя в Інтернеті захищено.
Що таке шифрування RSA?
Скажімо, ви хочете розповісти своєму другу секрет. Якщо ви поруч із ними, можете просто прошепотіти. Якщо ви перебуваєте на протилежних сторонах країни, це, очевидно, не вийде. Ви можете записати його і надіслати їм пошту або скористатися телефоном, але кожен із цих каналів зв’язку є небезпечним і кожен, хто має достатньо сильну мотивацію, може легко перехопити повідомлення.
Якщо секрет був досить важливим, ви не ризикували б його нормально записати – шпигуни або працівник поштового зв’язку може переглядати вашу пошту. Так само, хтось може натискати на ваш телефон без вашого відома і здійснювати реєстрацію кожного кожного дзвінка, який ви здійснюєте.
Одним із варіантів запобігання доступу підслуховувачів до вмісту повідомлення є зашифруйте його. Це в основному означає додати код до повідомлення, який перетворює його на змішаний безлад. Якщо ваш код достатньо складний, то лише ті, хто зможе отримати доступ до оригінального повідомлення, – це ті, хто має доступ до коду.
Якщо у вас був шанс поділитися кодом зі своїм другом заздалегідь, то будь-хто з вас може надіслати зашифроване повідомлення в будь-який час, знаючи, що ви двоє – єдині, хто має можливість читати вміст повідомлення. Але що робити, якщо ви раніше не мали шансу поділитися кодом?
Це одна з фундаментальних проблем криптографії, яку вирішив схеми шифрування відкритим ключем (також відомі як асиметричне шифрування) на зразок RSA.
Під шифруванням RSA повідомлення шифруються кодом під назвою a відкритий ключ, якими можна ділитися відкрито. Завдяки деяким виразним математичним властивостям алгоритму RSA, після того, як повідомлення зашифроване відкритим ключем, його можна розшифрувати лише іншим ключем, відомим як приватний ключ. У кожного користувача RSA є пара ключів, що складається з їх публічних та приватних ключів. Як випливає з назви, приватний ключ повинен зберігатися в таємниці.
Схеми шифрування відкритого ключа відрізняються від шифрування симетричного ключа, де і в процесі шифрування, і в дешифруванні використовується один і той же приватний ключ. Ці відмінності роблять шифрування відкритих ключів на зразок RSA корисним для спілкування в ситуаціях, коли попередньо не було можливості безпечно поширювати ключі..
Алгоритми симетричних ключів мають власні програми, такі як шифрування даних для особистого використання, або для наявності захищених каналів, якими можна ділитися приватними ключами.
Дивись також: Криптографія відкритого ключа
Де використовується шифрування RSA?
Шифрування RSA часто використовується в поєднання з іншими схемами шифрування, або за цифрові підписи що може підтвердити справжність та цілісність повідомлення. Зазвичай він не використовується для шифрування цілих повідомлень або файлів, тому що він менш ефективний і більш важкий для ресурсів, ніж шифрування симетричного ключа.
Щоб зробити речі більш ефективними, файл, як правило, буде зашифрований алгоритмом симетричного ключа, і тоді симетричний ключ буде зашифрований за допомогою шифрування RSA. Під час цього процесу лише об’єкт, який має доступ до приватного ключа RSA, зможе розшифрувати симетричний ключ.
Не маючи доступу до симетричного ключа, оригінальний файл неможливо розшифрувати. Цей метод може бути використаний для захисту повідомлень і файлів у безпеці, не забираючи занадто довго і не витрачаючи занадто багато обчислювальних ресурсів.
Шифрування RSA можна використовувати в декількох різних системах. Він може бути реалізований у OpenSSL, wolfCrypt, cryptlib та ряді інших криптографічних бібліотек.
Як одна з перших широко застосовуваних схем шифрування відкритим ключем, RSA заклала основи більшості наших безпечних комунікацій. Це було традиційно використовується в TLS також був оригінальним алгоритмом, використовуваним у шифруванні PGP. RSA все ще спостерігається у ряді веб-браузерів, електронної пошти, VPN, чату та інших каналів зв’язку.
RSA також часто використовується для забезпечення безпечного з’єднання між VPN-клієнтами та VPN-серверами. У таких протоколах, як OpenVPN, рукостискання TLS можуть використовувати алгоритм RSA для обміну ключами та встановлення захищеного каналу.
Передумови шифрування RSA
Як ми вже згадували на початку цієї статті, перед шифруванням відкритим ключем викликом було безпечне спілкування, якщо раніше не було можливості безпечно обмінятися ключами. Якщо раніше не було можливості ділитися кодом або захищеним каналом, через який можна було поширювати ключі, не було можливості спілкуватися без загрози, що вороги зможуть перехопити та отримати доступ до вмісту повідомлення.
Тільки в 1970-х роках все почало змінюватися. Перша велика розробка до того, що ми сьогодні називаємо криптографією з відкритим ключем, була опублікована на початку десятиліття Джеймсом Х. Еллісом. Елліс не міг знайти спосіб втілити свою роботу, але його колега Кліффорд Кокс розширила його, щоб стати тим, що ми тепер знаємо як Шифрування RSA.
Заключний фрагмент головоломки – це те, що ми зараз називаємо Обмін ключами Diffie-Hellman. Малкольм Дж. Вільямсон, інший колега, придумав схему, яка дозволила двом сторонам ділитися ключем шифрування, навіть якщо канал контролювали супротивники.
Вся ця робота проводилась у розвідувальному агентстві Великобританії, штаб-квартирі уряду з питань комунікацій (GCHQ), який зберігав відкриття класифікованим. Частково через технологічні обмеження GCHQ не могла побачити використання криптографії з відкритим ключем у той час, тому розробка простоювала на полиці, збираючи пил. Тільки в 1997 році твір було розсекречено і первісні винахідники RSA були визнані.
Через кілька років подібні концепції почали розвиватися в публічній сфері. Ральф Меркле створив ранню форму криптографія з відкритим ключем, що вплинуло на Вітфілда Діффі та Мартіна Гелмана на розробку обміну ключами Діффі-Геллмана.
Ідеї Діффі та Гелмана бракували одного важливого аспекту, який зробив би їхню основу криптографією відкритого ключа. Це був а одностороння функція, яку важко було б інвертувати. У 1977 році, Рон Рівест, Аді Шамір та Леонард Адлеман, прізвища яких складають абревіатуру RSA, придумали рішення після року роботи над проблемою.
Академіки на базі MIT здійснили свій прорив після Пасхальної вечірки у 1977 році. Після нічної випивки Рівест пішов додому, але замість того, щоб спати, він провів вечір гарячково, пишучи документ, який формалізував його ідею для необхідної однобічної функції.
Ідея була запатентована в 1983 році MIT, але лише в перші дні Інтернету алгоритм RSA почав сприймати широке прийняття як важливий інструмент безпеки.
Як працює шифрування RSA?
Далі буде трохи спрощення, тому що занадто багато читачів, мабуть, були злякані своїм вчителем математики середньої школи. Щоб математика не надто виходила з рук, ми будемо спрощення деяких понять та використання значно менших чисел. Насправді шифрування RSA використовує прості числа, які значно більші за величиною, і є кілька інших складностей.
Існує кілька різних концепцій, які вам доведеться обійти, перш ніж ми зможемо пояснити, як все це поєднується. До них відносяться функціональні функції, що генерують праймери, підкреслює функцію Кармікеля і окремих процесів, що беруть участь у обчислення відкритого та приватного ключів використовується в процесах шифрування та дешифрування.
Функції дверних пасток
Шифрування RSA працює за умови, що алгоритм є легко обчислити в одному напрямку, але майже неможливо в зворотному напрямку. Як приклад, якби вам сказали, що 701,111 – це добуток двох простих чисел, ви зможете зрозуміти, що це за два числа?
Навіть з калькулятором чи комп’ютером більшість із нас не мали б уявлення з того, з чого почати, не кажучи вже про те, щоб зрозуміти відповідь. Але якщо ми перевернемо речі, це стане набагато простіше. Які результати:
907 x 773
Якби вам було нудно, ви змогли б вирвати телефон або, можливо, порахувати його в голові, щоб виявити, що відповідь – це вже згадуваний раніше 701,111. Ці 907 та 773 – це прості числа, які відповідають на наше перше запитання, яке показує нам, що певні рівняння можна легко зрозуміти одним способом, але, здається, неможливими у зворотному напрямку.
Ще один цікавий аспект цього рівняння полягає в тому, що легко визначити одне з простих чисел, якщо у вас вже є друге, а також добуток. Якщо вам скажуть, що 701,111 є результатом 907, помноженим на інше просте число, ви можете визначити його іншим простим числом із наступним рівнянням:
701,111 ÷ 907 = 773
Оскільки відношення між цими числами просто обчислити в одному напрямку, але неймовірно важке в зворотному, рівняння відоме як функція дверних пасток. Будьте в курсі, що, хоча вищенаведений приклад важко зрозуміти людям, комп’ютери можуть робити операцію в тривіальній кількості часу.
Через це RSA використовує значно більші числа. Розмір праймерів у реальній реалізації RSA змінюється, але в 2048-бітному RSA вони зійдуться, щоб зробити ключі довжиною 617 цифр. Щоб допомогти вам візуалізувати це, ключовим буде номер такого розміру:
99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999
Утворення прайметів
Згадані вище функції дверних пасток складають основу для роботи схем шифрування відкритого та приватного ключа. Їх властивості дозволяють ділитися відкритими ключами, не загрожуючи повідомленням або розкриваючи приватний ключ. Вони також дозволяють шифрувати дані одним ключем таким чином, що їх можна розшифрувати лише іншим ключем з пари.
Першим кроком шифрування повідомлення за допомогою RSA є згенерувати ключі. Для цього нам потрібно два простих числа (p і q) які відбираються за допомогою тесту на первинність. Тест первинності – це алгоритм, який ефективно знаходить прості числа, такі як тест первинності Рабіна-Міллера.
Прості числа в RSA повинні бути дуже великими, а також відносно далекими. Малі чи невеликі численні цифри набагато простіше зламати. Незважаючи на це, у нашому прикладі будуть використані менші числа, щоб полегшити процес прослідування та обчислення.
Скажімо, тест на первинність дає нам прості числа, які ми використовували вище, 907 та 773. Наступним кроком є розкриття модуля (н), використовуючи таку формулу:
н = p х q
Де p = 907 і q = 773
Тому:
н = 907 х 773
н = 701,111
Томічна функція Кармайхеля
Раз у нас є н, ми використовуємо Томічна функція Кармікеля:
λ(н) = lcm (p – 1, q – 1)
Якщо минуло час, коли ви потрапили в підручники з математики, вищезгадане може виглядати трохи жахливо. Ви можете пропустити цю частину і просто довіряти, що математика працює, інакше дотримуйтесь нас для ще кількох розрахунків. Все буде пояснено якомога детальніше, щоб допомогти вам осягнути основи.
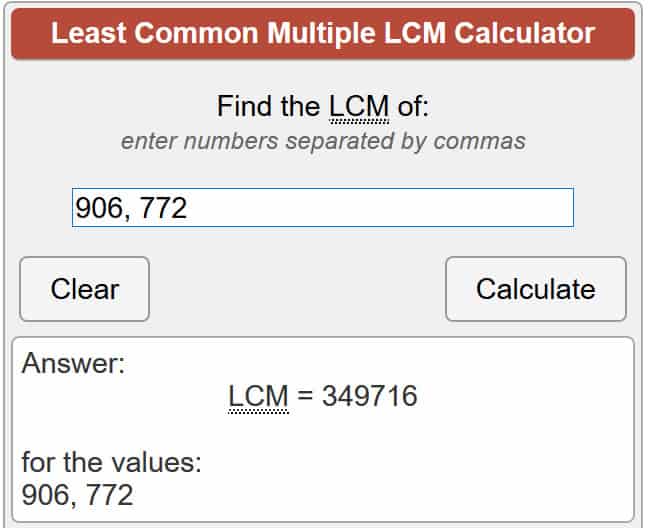
Для тих, хто не знає, λ (n) репрезентує Томік для Кармікеля н, поки lcm означає найменший загальний кратний, що є найнижчим числом, що обидва p і q може поділитися на. Існує кілька різних способів вирішити це, але найпростіше – довірити онлайн-калькулятору, щоб зробити рівняння за вас. Тож давайте введемо наші числа в рівняння:
λ(701,111) = lcm (907 – 1, 773 – 1)
λ(701,111) = lcm (906, 772)
Використовуючи приєднаний вище калькулятор, це дає нам:
λ(701,111) = 349 716
Створення відкритого ключа
Тепер, коли у нас є найвищий номер Carmichael, це – час з’ясувати наш відкритий ключ. За RSA, відкриті ключі складаються з простого числа е, так само, як н. Кількість е може бути що-небудь між 1 і значенням для λ(н), що в нашому прикладі становить 349 716.
Оскільки відкритий ключ відкрито ділиться, це не так важливо е бути випадковим числом. На практиці, е як правило, встановлено на 65,537, адже коли набагато більші числа вибираються випадковим чином, це робить шифрування набагато менш ефективним. На сьогоднішньому прикладі ми збережемо малі цифри, щоб зробити обчислення ефективними. Скажімо:
е = 11
Наші остаточні зашифровані дані називаються шифротекстом (c). Ми отримуємо це з нашого простого повідомлення (м), застосувавши відкритий ключ у такій формулі:
c = ме мод н
Ми вже придумали е і ми знаємо н так само. Єдине, що нам потрібно пояснити, – це мод. Це трохи вийшло з глибини цієї статті, але це стосується а модульна операція, що по суті означає залишок, що залишився, коли ви розділяєте одну сторону на іншу. Наприклад:
10 мод 3 = 1
Це тому, що 3 тричі переходить у 10, а решта – 1.
Повернутися до нашого рівняння. Щоб все було просто, скажімо так повідомлення (м), що ми хочемо зашифрувати і зберегти в секреті – це лише одне число, 4. Давайте підключимо все:
c = ме мод н
c = 411 мод 701,111
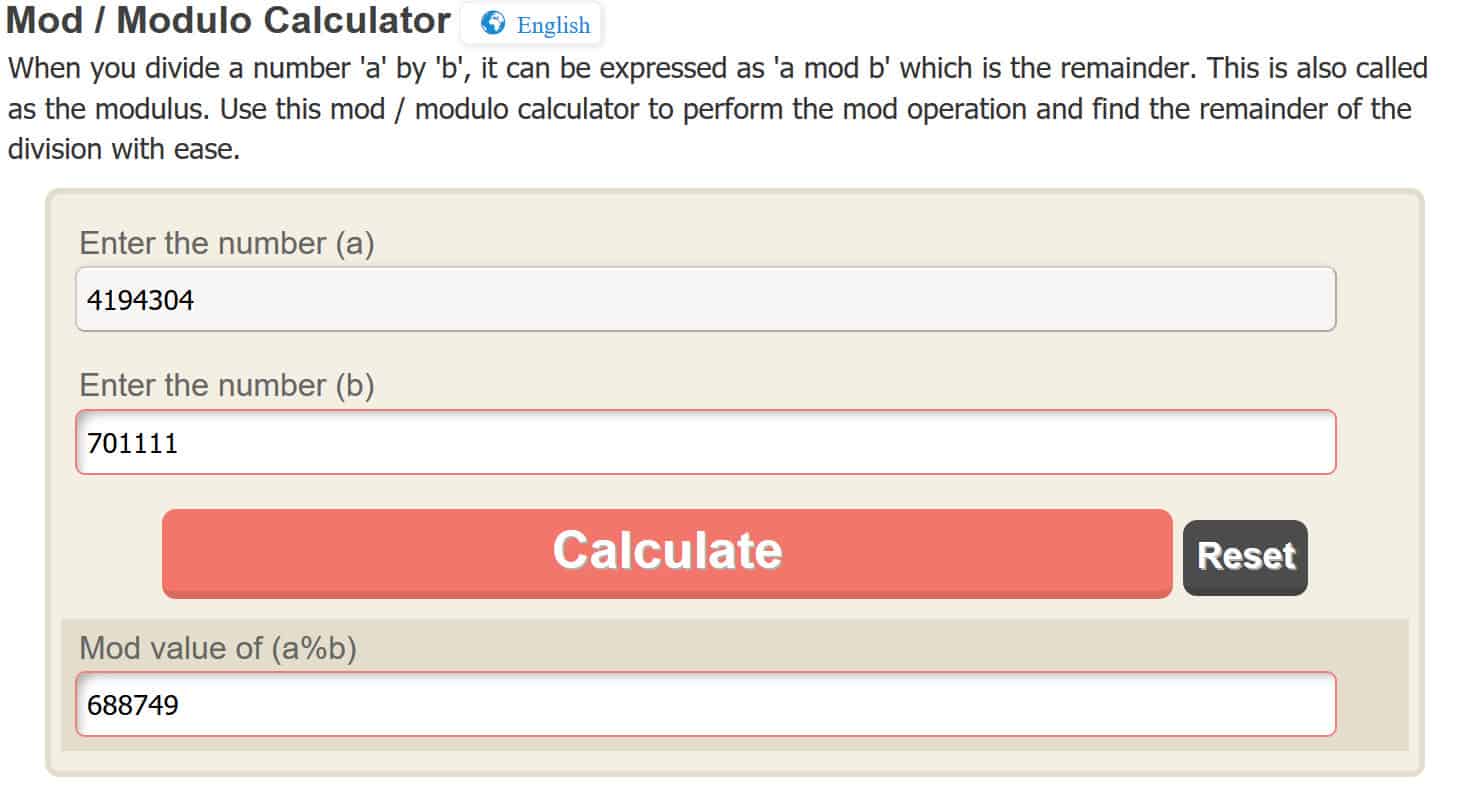
c = 4,194,304 мод 701,111
Знову, щоб зробити модульна операція легко, ми будемо користуватися онлайн-калькулятором, але ви можете розібратися в цьому самі. Ввівши 4,194,304 в онлайн-калькулятор, він дає нам:
c = 688,749
Тому, коли ми використовуємо RSA для шифрування нашого повідомлення, 4, за допомогою нашого відкритого ключа, він дає нам шифротекст 688 749. Попередні кроки могли здатися занадто важкими для математики, але важливо повторити, що насправді сталося.
У нас був повідомлення 4, яку ми хотіли зберегти в таємниці. Ми застосували до нього відкритий ключ, який надав нам зашифрований результат 688 749. Тепер, коли він зашифрований, ми можемо надійно надіслати номер 688 749 власнику пари ключів. Вони єдина людина, яка зможе розшифрувати його своїм приватним ключем. Коли вони розшифрують його, вони побачать повідомлення, яке ми насправді надсилали, 4.
Створення приватного ключа
У шифруванні RSA, коли дані або повідомлення перетворюються на шифротекст із відкритим ключем, його можна розшифрувати лише приватним ключем із тієї ж пари ключів. Приватні ключі складаються з г і н. Ми вже знаємо н, і для знаходження використовується наступне рівняння г:
г = 1 /е мод λ(н)
В Створення відкритого ключа Розділ вище, ми вже вирішили це на нашому прикладі, е дорівнювало б 11. Так само ми це знаємо λ(н) дорівнює 349 716 з нашої попередньої роботи в Томічна функція Кармайхеля. Все стає трохи складніше, коли ми стикаємося з цим розділом формули:
1 /е мод
Це рівняння може виглядати так, що воно просить розділити 1 на 11, але це не так. Натомість це просто символізує, що нам потрібно обчислити модульна обернена з е (що в цьому випадку 11) та λ(н) (що в даному випадку становить 349 716).
Це по суті означає це замість виконання стандартної операції по модулю, ми будемо використовувати зворотний. Зазвичай це зустрічається з розширеним евклідовим алгоритмом, але це трохи виходить за рамки цієї статті, тому ми просто обдуримо і використаємо онлайн-калькулятор. Тепер, коли ми розуміємо все, що відбувається, давайте включимо нашу інформацію у формулу:
г = 1 /11 мод 349 716
Щоб виконати цю операцію, просто введіть 11 (або будь-яке значення, яке може бути у вас для е якщо ви намагаєтесь це на власному прикладі), де це сказано Цілий і 349 716 (або будь-яке значення, яке може мати для вас λ(н) якщо ви намагаєтеся це на власному прикладі), де це сказано Модуло в онлайн-калькуляторі, який був пов’язаний вище. Якщо ви це зробили правильно, ви повинні отримати результат, коли:
г = 254, 339
Тепер, коли ми маємо значення для г, ми можемо розшифрувати повідомлення, які були зашифровані нашим відкритим ключем, використовуючи наступну формулу:
м = cг мод н
Тепер ми можемо повернутися до шифротексту, який ми зашифрували під Створення приватного ключа розділ. Коли ми зашифрували повідомлення відкритим ключем, воно дало нам значення c з 688 749. Зверху ми це знаємо г дорівнює 254,339. Ми також це знаємо н дорівнює 701,111. Це дає нам:
м = 688 749254,339 мод 701,111.
Як ви могли помітити, спроба прийняти число до 254,339-ї потужності може бути трохи більшою мірою для звичайних калькуляторів. Натомість ми будемо використовувати онлайн-калькулятор розшифровки RSA. Якби ви хотіли скористатися іншим методом, ви застосували б повноваження, як зазвичай, і виконали операцію з модулем так само, як і в Створення відкритого ключа розділ.
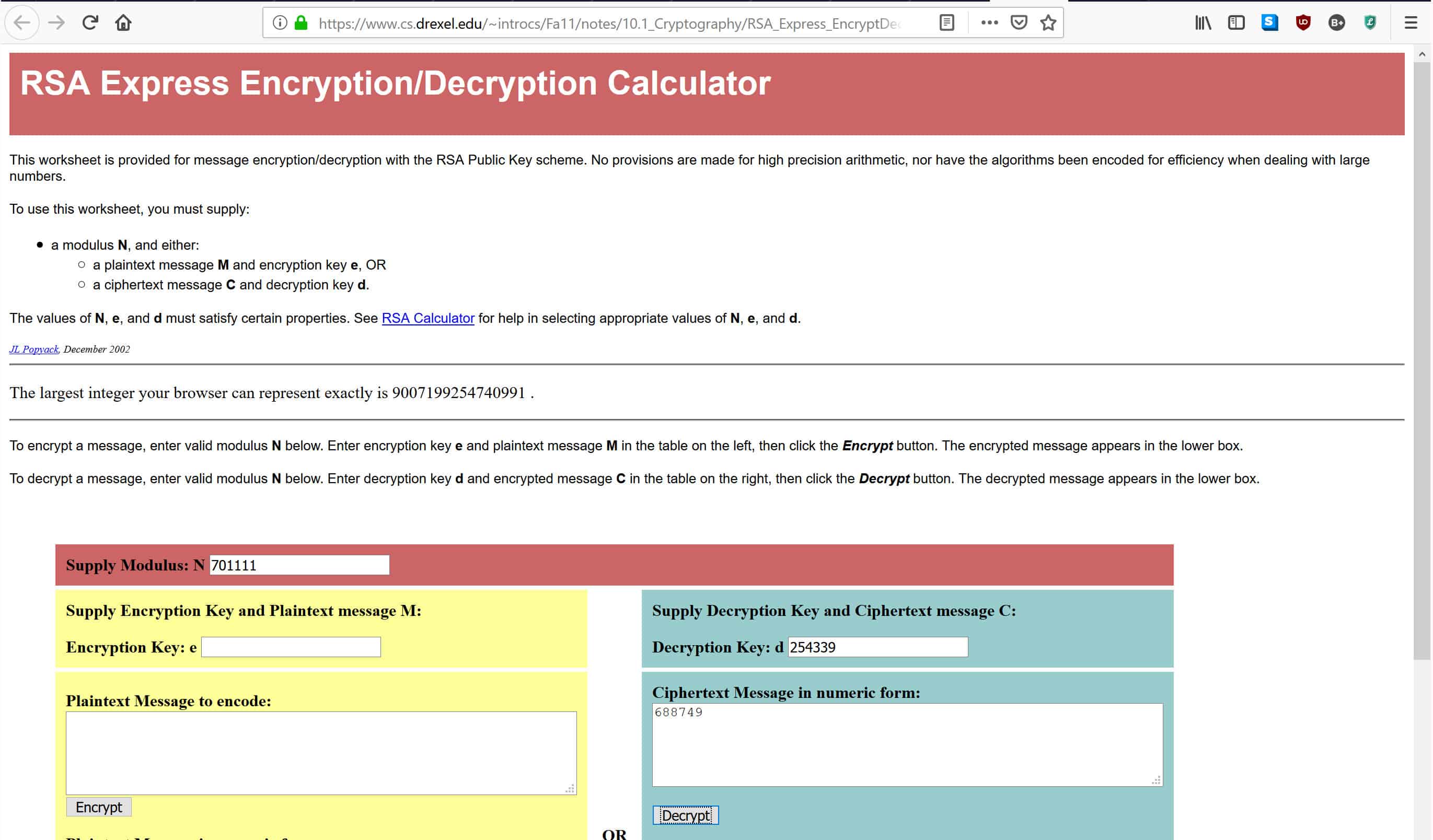
У калькулятор, пов’язаний вище, введіть 701,111, де написано Модуль постачання: N, 254 399, де написано Ключ розшифровки: D, і 688 749, де йдеться Повідомлення шифротексту в числовій формі, як показано нижче:
Після введення даних натисніть Розшифруйте, який поставить числа через формулу дешифрування, яка була перерахована вище. Це дасть вам оригінальне повідомлення в полі нижче. Якщо ви все зробили правильно, вам слід отримати відповідь 4, яке було оригінальним повідомленням, яке ми зашифрували своїм відкритим ключем.
Як працює шифрування RSA на практиці
Наведені вище розділи повинні дати зрозуміти, як працює математика шифрування відкритого ключа. Це може бути трохи заплутано, але навіть ті, хто не розумів тонкощів рівнянь, можуть, сподіваючись, забрати важливу інформацію про процес.
На етапах, перелічених вище, ми показали, як два об’єкти можуть безпечно спілкуватися, не попередньо ділившись кодом. По-перше, кожен з них повинен створити власні пари ключів і ділитися відкритим ключем один з одним. Дві особи повинні зберігати свої секретні ключі в секреті, щоб їх зв’язок залишався в безпеці.
Щойно відправник має відкритий ключ свого одержувача, він може використовувати його для шифрування даних, які вони хочуть захистити. Після того, як він зашифрований відкритим ключем, його можна розшифрувати лише приватним ключем з тієї ж пари ключів. Навіть той самий відкритий ключ не можна використовувати для дешифрування даних. Це пов’язано з властивостями функції дверних пасток що ми згадували вище.
Коли одержувач отримує зашифроване повідомлення, вони використовують свій приватний ключ для доступу до даних. Якщо одержувач хоче повернути повідомлення безпечним способом, вони можуть зашифрувати своє повідомлення відкритим ключем партії, з якою вони спілкуються. Знову ж таки, після шифрування відкритим ключем єдиний спосіб доступу до інформації – це відповідний приватний ключ.
Таким чином, шифрування RSA може використовуватися невідомими раніше сторонами для надійної передачі даних між собою. З цієї основи були створені значні частини комунікаційних каналів, які ми використовуємо в нашому житті в Інтернеті.
Як складніші повідомлення шифруються за допомогою RSA?
У нашому прикладі ми багато спростили речі, щоб полегшити їх розуміння, тому ми лише зашифрували повідомлення “4”. Вміти зашифрувати число 4 не здається особливо корисним, тому вам може бути цікаво як можна зашифрувати більш складний набір даних, наприклад, симетричний ключ (який найчастіше використовується RSA) або навіть повідомлення.
Деякі люди можуть бути здивовані тим, як ключ на зразок “n38cb29fkbjh138g7fqijnf3kaj84f8b9f …” або повідомлення типу “купити мені сендвіч” можна зашифрувати за допомогою алгоритму типу RSA, який має справу з цифрами, а не літерами. Реальність полягає в тому, що вся інформація, яку обробляють наші комп’ютери, зберігається у двійковій (1s і 0s), і ми використовуємо стандарти кодування, такі як ASCII або Unicode представляти їх способами, які люди можуть зрозуміти (букви).
Це означає що такі клавіші, як “n38cb29fkbjh138g7fqijnf3kaj84f8b9f …”, а такі повідомлення, як “купити мені сендвіч”, вже існують як номери, який легко можна обчислити в алгоритмі RSA. Цифри, якими вони представлені, нам набагато більші і важче керувати, тому ми вважаємо за краще мати справу з буквено-цифровими символами, а не зі спалахом двійкових.
Якби ти хотів зашифруйте більш довгий ключ сеансу або більш складне повідомлення з RSA, це просто включатиме набагато більшу кількість.
Прокладки
Коли RSA реалізований, він використовує щось, що називається накладки для запобігання ряду атак. Щоб пояснити, як це працює, почнемо з прикладу. Скажімо, ви надіслали другу закодоване повідомлення:
Шановна Карен,
Я сподіваюся, що з тобою все в порядку. Ми ще завтра вечеряємо??
Щиро Ваш,
Джеймс
Скажімо, ви кодували повідомлення простим способом змінюючи кожну букву на ту, що йде за нею в алфавіті. Це змінює повідомлення на:
Efbs Lbsfo,
J ipqf zpv bsf xfmm. Bsf xf tujmm ibwjoh ejoofs upnpsspx?
Zpvst tjodfsfmz,
Kbnft
Якщо ваші вороги перехопили цей лист, є хитрість, яку вони можуть використати, щоб спробувати зламати код. Вони могли б подивіться на формат вашого листа і спробуйте відгадати, про що може говорити повідомлення. Вони знають, що люди зазвичай починають свої листи з “Привіт”, “Привіт”, “Шановний” або з низкою інших конвенцій.
Якби вони спробували застосувати “Привіт” або “Привіт” як перше слово, вони побачили б, що це не відповідає кількості символів. Потім вони можуть спробувати “Шановний”. Це підходить, але це не обов’язково нічого означає. Зловмисники просто спробували б це і побачили, куди це їх привело. Таким чином вони будуть змінювати літери “е”, “f”, “b” і “s” на “d”, “e”, “a” і “r” відповідно. Це дало б їм:
Шановний Ласео,
J ipqe zpv – xemm. Чи xe tujmm iawjoh djooes upnpsspx?
Zpvrt tjoderemz,
Канет
Це все ще виглядає досить заплутано, тому зловмисники можуть спробувати переглянути деякі інші умовності, як, як ми укладаємо наші листи. Люди часто додають “З” або “З повагою” наприкінці, але жодне з них не відповідає формату. Натомість зловмисники можуть спробувати “З повагою” і замінити інші букви, щоб побачити, де вони потрапляють. Змінюючи “z”, “p”, “v”, “t”, “j” “o”, “d” і “m” на “y”, “o”, “u”, “s”, ” i “,” n “,” c “і” l “відповідно, вони отримають:
Шановний Ласен,
I ioqe ви xell. Чи xe tuill iawinh dinnes uonossox?
Щиро Ваш,
Канет
Після цієї модифікації схоже, що зловмисники починають кудись потрапляти. Вони знайшли слова “я”, “ти” і “є”, крім слів, які складали їхні початкові здогадки.
Бачачи, як слова в правильному граматичному порядку, зловмисники можуть бути досить впевнені, що вони прямують у правильному напрямку. На сьогоднішній день вони, ймовірно, також зрозуміли, що код передбачає зміну кожної літери на ту, що йде за нею в алфавіті. Як тільки вони зрозуміють це, це легко перекладати решту та прочитати оригінальне повідомлення.
Наведений вище приклад був просто простим кодом, але як ви бачите, структура повідомлення може давати зловмисникам підказки щодо його вмісту. Звичайно, було важко розібратися з повідомленням лише з його структури, і для цього знадобилися певні здогадки, але потрібно пам’ятати, що комп’ютери набагато краще це роблять, ніж ми. Це означає, що їх можна використовувати для з’ясування набагато складніших кодів за набагато коротший час, заснований на підказках, що походять від будови та інших елементів.
Якщо структура може призвести до розтріскування коду та розкриття вмісту повідомлення, тоді нам потрібен певний спосіб приховати структуру, щоб зберегти повідомлення в безпеці. Це приводить нас до підкладка.
Коли повідомлення прокладене, Додані рандомізовані дані, щоб приховати оригінальні підказки форматування, які можуть призвести до розбиття зашифрованого повідомлення. З RSA справи дещо складніші, тому що зашифрований ключ не має очевидного форматування листа, що допомогло б дати нам підказки у нашому вище прикладі.
Незважаючи на це, противники можуть використовувати ряд атак для використання математичних властивостей коду та розбиття зашифрованих даних. Через цю загрозу, реалізація RSA використовують схеми заміщення, такі як OAEP, для вбудовування додаткових даних у повідомлення. Додавання цієї підкладки перед шифруванням повідомлення робить RSA набагато безпечнішим.
Підписання повідомлень
RSA можна використовувати для шифрування даних, ніж просто. Його властивості також роблять його корисною системою підтвердження того, що повідомлення було надіслано особою, яка заявляє, що його надіслало, а також доводить, що повідомлення не було змінено або підроблено.
Коли хтось хоче довести справжність свого повідомлення, він може обчислити: хеш (функція, яка приймає дані довільного розміру і перетворює їх у значення фіксованої довжини) простого тексту, а потім підписує їх своїм приватним ключем. Вони підпишіть хеш, застосовуючи ту саму формулу, яка використовується при дешифруванні (m = cг мод н). Після підписання повідомлення вони надсилають цей цифровий підпис одержувачу разом із повідомленням.
Якщо одержувач отримує повідомлення з цифровим підписом, він може використовувати підпис, щоб перевірити, чи було повідомлення справді підписане приватним ключем особи, яка стверджує, що його надіслала. Вони також можуть бачити, чи змінилося повідомлення нападниками після його надсилання.
Для перевірки цифрового підпису одержувач спочатку використовує ту саму хеш-функцію, щоб знайти хеш-значення отриманого ними повідомлення. Потім одержувач застосовує відкритий ключ відправника до цифрового підпису, використовуючи формулу шифрування (c = mе mod n), щоб дати їм хеш цифрового підпису.
За порівнюючи хеш повідомлення, яке було отримано поряд із хешем від зашифрованого цифрового підпису, одержувач може сказати, чи є повідомлення автентичним. Якщо два значення однакові, повідомлення не було змінено з моменту його підписання від оригінального відправника. Якби повідомлення було змінено навіть одним символом, значення хеша було б зовсім іншим.
Безпека RSA & напади
Як і більшість криптосистем, безпека RSA залежить від того, як вона реалізована та використовується. Одним з важливих факторів є розмір ключа. The чим більша кількість бітів у ключі (по суті, наскільки довгий ключ), тим складніше зламати атаки такі як груба форсинг та факторинг.
Оскільки алгоритми асиметричних ключів, такі як RSA, можуть бути порушені цілочисловою факторизацією, тоді як алгоритми симетричних ключів, такі як AES, не можуть, ключі RSA повинні бути набагато довші, щоб досягти однакового рівня безпеки.
В даний час Найбільший розмір ключів, який було задіяно, – 768 біт. Це було зроблено командою вчених протягом двох років, використовуючи сотні машин.
Оскільки факторинг був завершений до кінця 2009 року і обчислювальна потужність значно зросла з того часу, можна припустити, що спроба аналогічної інтенсивності тепер може враховувати значно більший ключ RSA.
Незважаючи на це, час і ресурси, необхідні для подібного нападу, виводять його з-за межі досяжності більшості хакерів і перебувають у царині національних держав. Найкраща тривалість використання ключа залежатиме від вашої індивідуальної моделі загрози. Національний інститут стандартів та технологій рекомендує мінімальний розмір ключа 2048-біт, але також використовуються 4096-бітні клавіші в деяких ситуаціях, коли рівень загрози вищий.
Факторинг – лише один із способів розбити RSA. Ряд інших атак може потенційно порушити шифрування за рахунок меншої кількості ресурсів, але вони залежать від реалізації та інших факторів, не обов’язково самих RSA. Деякі з них включають:
Чи справді випадкові прими?
Деякі реалізації RSA використовують слабкі генератори випадкових чисел, щоб придумати праймери. Якщо ці цифри не є достатньо випадковими, зловмисникам значно полегшується їх розміщення факторами і порушенням шифрування. Ця проблема можна уникнути, використовуючи криптографічно захищений генератор псевдовипадкових чисел.
Погане покоління ключів
Ключі RSA повинні підпадати під певні параметри, щоб вони були захищені. Якщо праймери p і q занадто близько один до одного, ключ можна легко знайти. Так само і число г що становить частину приватного ключа, не може бути надто маленьким. Низьке значення полегшує вирішення. Важливо, щоб ці номери були достатньої довжини, щоб захистити ваш ключ.
Атаки бічних каналів
Це тип атаки, який не порушує RSA безпосередньо, а замість цього використовує інформацію з його реалізації, щоб дати нападникам натяки на процес шифрування. Ці напади можуть включати такі речі аналіз кількості потужності, яка використовується, або аналіз прогнозування галузі, який використовує вимірювання часу виконання для виявлення приватного ключа.
Інший тип атаки бічних каналів відомий як атака синхронізації. Якщо зловмисник має можливість вимірювати час розшифровки на комп’ютері своєї цілі для кількох різних зашифрованих повідомлень, ця інформація може дати можливість зловмиснику визначити приватний ключ цілі.
Більшість реалізацій RSA уникають цієї атаки, додаючи одноразове значення під час процесу шифрування, що видаляє це співвідношення. Цей процес називається криптографічне осліплення.
Чи безпечне шифрування RSA для майбутнього?
Хороша новина полягає в тому, що RSA вважається безпечним для використання, незважаючи на ці можливі атаки. Застереження в тому її потрібно правильно реалізувати і використовувати ключ, що підпадає під правильні параметри. Як ми вже обговорювали, реалізація, яка не використовує прокладки, використовує праймери неадекватного розміру або мають інші вразливості, не може вважатися безпечною..
Якщо ви хочете використовувати шифрування RSA, переконайтеся, що ви використовуєте ключ принаймні 1024 біт. Ті, хто має більш високу загрозу, повинні дотримуватися клавіш 2048 або 4096 біт, якщо вони хочуть впевнено використовувати RSA. Поки ви усвідомлюєте слабкі сторони, якими володіє RSA, і правильно їх використовуйте, ви повинні почуватись безпечно використовувати RSA для спільного використання ключів та інших подібних завдань, які вимагають шифрування відкритих ключів..
Дивись також: Пояснено загальні типи шифрування