Що таке обмін ключами Diffie – Hellman і як це працює?

Обмін ключами Діффі-Гелмана був одна з найважливіших розробок криптографії з відкритим ключем і він все ще часто реалізовується в різних сучасних протоколах безпеки.

Це дозволяє двом сторонам, які раніше не зустрічалися, надійно встановити ключ, який вони можуть використовувати для захисту своїх комунікацій. У цій статті ми пояснимо, для чого вона використовується, як вона працює поетапно, її різні варіанти, а також міркування щодо безпеки, які потрібно врахувати, щоб безпечно її реалізувати..

Що таке обмін ключами Diffie-Hellman?

Обмін ключами Діффі-Гелмана був перший широко застосовуваний метод безпечної розробки та обміну ключами по незахищеному каналу.

Це не може здатися настільки захоплюючим або новаторським у вищезазначених термінах, тому давайте приклад, який пояснює, чому обмін ключами Діффі-Хеллмана був таким важливим етапом у світі криптографії та чому він досі так часто використовується.

Скажімо, ви – найпотаємніший шпигун, і вам потрібно надіслати важливу інформацію до вашого штабу. Як би ви не завадили ворогам отримати повідомлення?

Найпоширенішим рішенням буде шифрування повідомлення кодом. Найпростіший спосіб – впорядкувати будь-який тип коду та ключ, який ви плануєте використовувати заздалегідь, або зробити це через безпечний канал зв’язку.

Скажімо, ви особливо поганий шпигун, і ви та ваш штаб вирішили використовувати слабкий шифр зсуву для кодування ваших повідомлень. У цьому коді кожен “a” стає “b”, кожен “b” стає “c”, кожен “c” стає “d” і так далі, аж до “z”, що стає “a”.

Під цим шифром зсуву повідомлення “Давай пообідати” стає “Mfu’t hfu ejoofs”. На щастя, у нашій гіпотетичній ситуації ваші супротивники настільки ж некомпетентні, як і ви, і не в змозі зламати такий простий код, який не дає їм доступу до вмісту повідомлення.

Але що станеться, якщо ви не змогли заздалегідь домовитись коду зі своїм одержувачем?

Скажімо, ви хочете спілкуватися зі шпигуном союзної нації, якого ви ніколи не зустрічали. У вас немає безпечного каналу, по якому можна спілкуватися з ними. Якщо ви не шифруєте своє повідомлення, то будь-який противник, який перехопить його, зможе прочитати вміст. Якщо ви зашифруєте його, не повідомивши коду союзника, то ворог не зможе його прочитати, але і союзник не буде.

Ця проблема була однією з найбільших загадок у криптографії до 1970-х років:

Як можна безпечно обмінюватися інформацією з кимось, якщо ви не мали можливості поділитися ключем достроково?

Обмін ключами Діффі-Гелмана був першим публічно використовуваним механізмом вирішення цієї проблеми. Алгоритм дозволяє тим, хто ніколи раніше не зустрічався, безпечно створювати загальний ключ, навіть через незахищений канал, який можуть контролювати супротивники.

Історія обміну ключами Діффі-Гелмана

Обмін ключами Діффі-Гелмана простежується корінням у 1970-ті роки. Незважаючи на те, що сфера криптографії суттєво розвивалася протягом початку ХХ століття, ці досягнення були зосереджені в основному на криптографії симетричного ключа.

Лише в 1976 році алгоритми відкритого ключа з’явилися у публічній сфері, коли Уїтфілд Діффі та Мартін Гелман опублікували свої статті, Нові напрямки в криптографії. Співпраця окреслила механізми нової системи, яка стала б відомою як ” Обмін ключами Diffie-Hellman.

Робота почасти була натхненна попередніми розробками, зробленими Ральфом Меркле. Так звані Головоломки Меркле залучайте одну сторону до створення та надсилання до інших криптографічних пазлів іншому. Ці головоломки потребували б вирішити невелику кількість обчислювальних ресурсів.

Одержувач випадковим чином вирішить одну головоломку для розв’язання, а потім витратить необхідні зусилля для її виконання. Після того, як головоломка буде вирішена, одержувачу розкриваються ідентифікатор та ключ сесії. Потім одержувач передає ідентифікатор назад початковому відправнику, що повідомляє відправнику знати, яка головоломка вирішена.

Оскільки оригінальний відправник створив головоломки, ідентифікатор дає їм знати, який ключ сеансу виявив одержувач, і дві сторони можуть використовувати цей ключ для більш безпечного спілкування. Якщо зловмисник прослуховує взаємодію, він отримає доступ до всіх головоломок, а також до ідентифікатора, який одержувач передає назад до оригінального відправника.

Ідентифікатор не вказує зловмиснику, який ключ сеансу використовується, тому найкращим підходом для розшифровки інформації є вирішити всі головоломки, щоб розкрити правильний ключ сесії. Оскільки зловмиснику доведеться розгадувати половину головоломок в середньому, виявити ключ набагато складніше, ніж для одержувача.

Такий підхід забезпечує більшу безпеку, але далеко не ідеальне рішення. Обмін ключами Diffie-Hellman взяв деякі з цих ідей і ускладнив їх для створення безпечного методу криптографії відкритого ключа.

Хоча це стало відомим як обмін ключами Diffie-Hellman, Мартін Геллман запропонував замість цього алгоритму назвати обмін ключами Diffie-Hellman-Merkle, щоб відобразити роботу, яку Ральф Меркле поставив над криптографією відкритого ключа.

Публічно вважалося, що Меркле, Хеллман і Діффі були першими людьми, які розробили криптографію відкритого ключа до 1997 року, коли британський уряд розсекретив роботу, виконану на початку 1970-х років Джеймс Елліс, Кліффорд Кокс та Малькольм Вільямсон.

Виявляється, тріо придумало першу схему шифрування з відкритим ключем між 1969 та 1973 роками, але їх роботу класифікували на два десятиліття. Він проводився під управлінням урядового штабу зв’язку (GCHQ), розвідувальним агентством Великобританії.

Їх відкриття насправді було алгоритмом RSA, тому Діффі, Геллман та Меркле все ще були першими, хто розробив обмін ключами Діффі-Геллмана, але вже не першими винахідниками криптографії відкритого ключа..

Де використовується обмін ключами Diffie-Hellman?

Основна мета обміну ключами Діффі-Гелмана – це надійно розробляти спільні секрети, які можна використовувати для отримання ключів. Потім ці клавіші можуть використовуватися з алгоритмами симетричних ключів для передачі інформації захищеним способом. Симетричні алгоритми, як правило, використовуються для шифрування основної маси даних, оскільки вони ефективніші, ніж алгоритми відкритого ключа.

Технічно обмін ключами Diffie-Hellman може використовуватися для встановлення відкритих та приватних ключів. Однак на практиці, як правило, використовується RSA. Це тому, що алгоритм RSA також здатний підписувати сертифікати відкритого ключа, тоді як обмін ключами Diffie-Hellman не є.

Алгоритм ElGamal, який широко використовувався в PGP, заснований на обміні ключових даних Diffie-Hellman, тому будь-який протокол, який його використовує, ефективно реалізує своєрідний Diffie-Hellman.

Одним із найпоширеніших методів безпечного розповсюдження ключів є обмін ключами Diffie-Hellman часто впроваджується в протоколи безпеки, такі як TLS, IPsec, SSH, PGP та багато інших. Це робить його невід’ємною частиною наших безпечних комунікацій.

Як частина цих протоколів, обмін ключами Diffie-Hellman часто використовується для захисту вашого зв’язку з веб-сайтом, для віддаленого доступу до іншого комп’ютера та для надсилання зашифрованих електронних листів

Як працює обмін ключами Diffie-Hellman?

Обмін ключами Diffie-Hellman є складним, і це може бути важко обійти головою, як це працює. Тут використовується дуже велика кількість і багато математики, щось, що багато хто з нас досі бояться від тих довгих і нудних уроків середньої школи.

Щоб зробити речі легшими для розуміння, ми почнемо з пояснення обміну ключами Діффі-Гелмана з аналогією. Як тільки ви зрозумієте, як воно працює, ми перейдемо до більш технічного опису основних процесів.

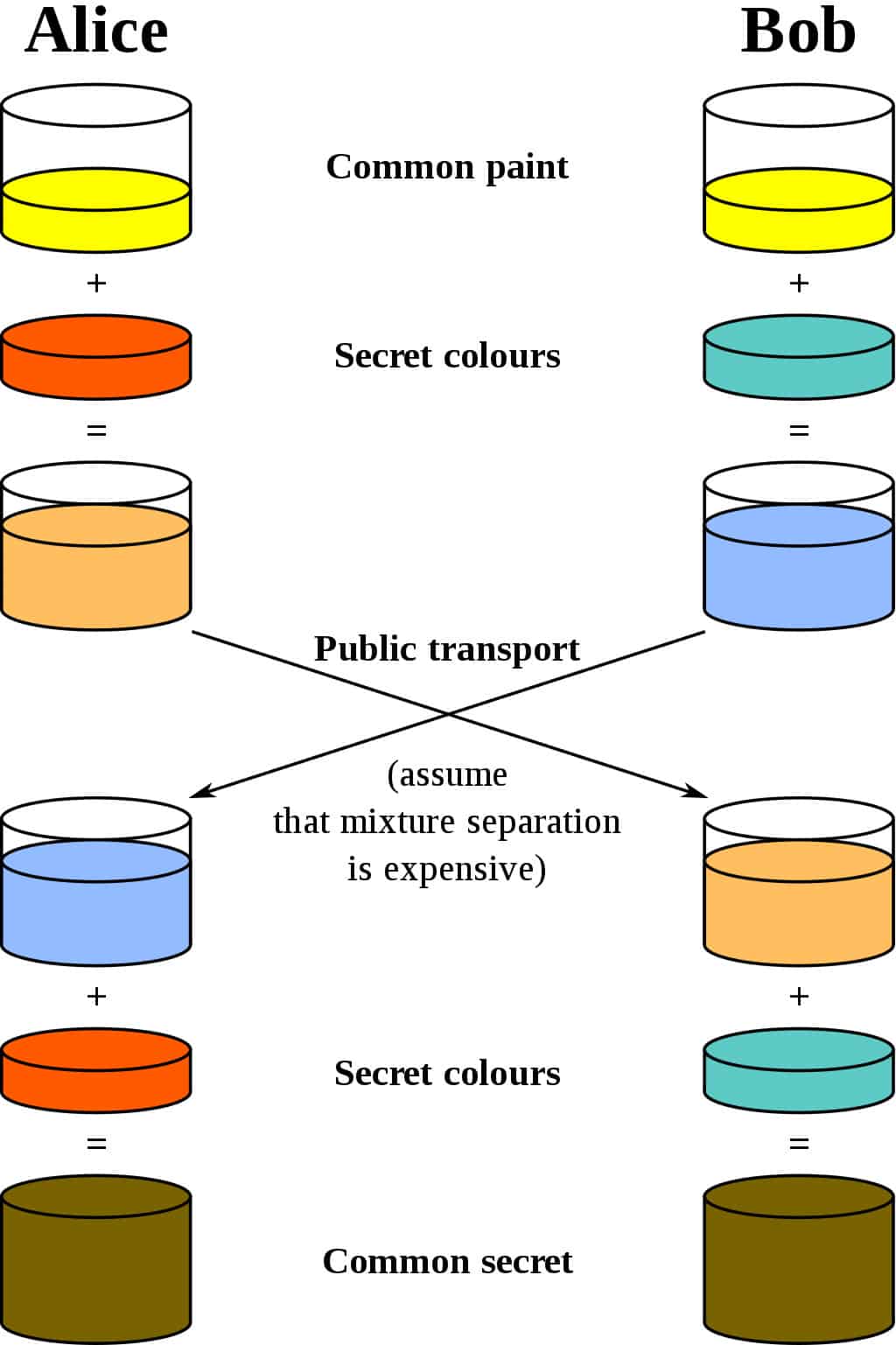
Найкраща аналогія для схеми Діффі-Гелмана – це продумати двоє людей, що змішують фарбу. Давайте скористаємося криптографічним стандартом і скажемо, що їх імена Аліса та Боб. Вони обидва домовляються про випадковий колір для початку. Скажімо, вони посилають один одному повідомлення і визначити жовтий як їх загальний колір, так само, як на схемі нижче:

вони мають свій секретний колір. Вони не говорять іншій стороні про свій вибір. Скажімо, що Аліса обирає червоний, поки Боб вибирає злегка зеленувато-синій.

Наступний крок – і Аліса, і Боб змішать свій таємний колір (червоний для Аліси, зеленувато-синій для Боба) з жовтим, про який вони взаємно домовлялися. Відповідно до діаграми, Аліса закінчується ан апельсинова суміш, а результат Боба – це глибший синій.

Після закінчення змішування вони надсилають результат іншій стороні. Аліса отримує глибший синій, поки Бобу надсилають фарбу помаранчевого кольору.

Після того, як вони отримали від партнера змішаний результат, вони додають йому свій секретний колір. Аліса бере глибший синій колір і додає свою таємну червону фарбу, поки Боб додає свою таємницю зеленувато-синього кольору до оранжевої суміші, яку він щойно отримав.

Результат? Вони обидва виходять одного кольору, що в даному випадку – огидне коричневе. Це може бути не той колір, яким ви хотіли б пофарбувати свою вітальню, але все-таки це загальний колір. Цей загальний колір називається ” загальна таємниця.

Найважливішою частиною обміну ключами Діффі-Гелмана є те, що обидві сторони отримують однаковий результат, не потребуючи жодного разу надсилати всю спільну таємницю по каналу зв’язку. Вибір загального кольору, власних таємних кольорів, обмін сумішшю, а потім додавання свого кольору ще раз дає обом сторонам спосіб дійти до одного і того ж загального секрету, не маючи необхідності надсилати всю справу.

Якщо зловмисник слухає обмін, все, до чого вони можуть отримати, – це звичайний жовтий колір, з якого починаються Аліса та Боб, а також змішані кольори, якими обмінюються. Оскільки це справді робиться з величезною кількістю замість фарби, цих відомостей недостатньо для нападу, щоб розпізнати будь-який початковий таємний колір, або загальну таємницю (технічно з цієї інформації можна обчислити загальну таємницю, але для безпечного впровадження обміну ключовими даними Діффі-Гелман знадобиться нездійсненна кількість часу та обчислювальних ресурсів для цього).

Ця структура обміну ключами Діффі-Гелмана – це те, що робить його таким корисним. Це дозволяє двом сторонам спілкуватися через потенційно небезпечний зв’язок і все ж придумувати спільний секрет, який вони можуть використовувати для створення ключів шифрування для своїх майбутніх комунікацій. Не має значення, чи слухають будь-які зловмисники, оскільки повний загальний секрет ніколи не надсилається через з’єднання.

Технічні деталі обміну ключами Diffie-Hellman

Час на математику …

Не хвилюйтесь, ми сприймемо це повільно і спробуємо зробити весь процес максимально легким для розуміння. Звідси випливає аналогічна передумова, як показана вище аналогія, але замість змішування та надсилання кольорів, схема Діффі-Гелмана фактично робить обчислення на основі виключно великих простих чисел, а потім надсилає їх поперек.

Для забезпечення безпеки рекомендується прайм (p) становить щонайменше 2048 біт, що є двійковим еквівалентом десяткового числа приблизно такого розміру:

415368757628736598425938247569843765827634879128375827365928736 84273684728938572983759283475934875938475928475928739587249587 29873958729835792875982795837529876348273685729843579348795827 93857928739548772397592837592478593867045986792384737826735267 3547623568734869386945673456827659498063849024875809603947902 7945982730187439759284620950293759287049502938058920983945872 0948602984912837502948019371092480193581037995810937501938507913 95710937597019385089103951073058710393701934701938091803984091804 98109380198501398401983509183501983091079180395810395190395180935 8109385019840193580193840198340918093851098309180019

Щоб уникнути вибуху кого-небудь голови, ми пояснимо це набагато меншою кількістю. Будьте в курсі цього обмін ключами Діффі-Гелмана був би невпевненним, якби він використовував числа, менші, ніж ті, що в нашому прикладі. Ми використовуємо лише такі невеликі числа, щоб продемонструвати концепцію більш простим способом.

У найпростішій формі обміну ключами Діффі-Гелмана, Еліс і Боб починаються, взаємно вирішуючи два числа, для початку, на відміну від єдиної звичайної фарби у наведеному вище прикладі. Це модуль (p) та основу (г).

У практичному використанні, модуль (p) – дуже велике просте число, поки основа (г) порівняно невелика для спрощення обчислень. Основа (г) є похідним від циклічної групи (Г), що зазвичай генерується задовго до того, як відбудуться інші кроки.

Для нашого прикладу скажімо, що модуль (p) є 17, в той час як база (г) є 4.

Після того як вони взаємно визначилися з цими номерами, Аліса встановлює секретний номер (а) для себе, поки Боб обирає свій секретний номер (б). Скажімо, що вони обирають:

a = 3

b = 6

Потім Аліса виконує такий розрахунок, щоб дати їй номер, який вона надішле Бобу:

A = ga mod p

У наведеному вище розрахунку, мод означає модульну операцію. Це по суті розрахунки, щоб з’ясувати залишок після ділення лівої сторони на праву. Як приклад:

15 мод 4 = 3

Якщо ви розумієте, як працюють модульні операції, можете зробити їх самостійно в наступних розрахунках, інакше ви можете скористатися онлайн-калькулятором.

Тож давайте введемо наші номери у формулу:

А = 43 мод 17

А = 64 мод 17

А = 13

Коли ми робимо те ж саме для Боба, ми отримуємо:

B = 46 мод 17

B = 4096 мод 17

B = 16

Потім Аліса надсилає свій результат (А) до Боба, поки Боб надсилає свою фігуру (Б) до Аліси. Потім Аліса обчислює загальний секрет (с), використовуючи номер, який вона отримала від Боба (Б) та її секретний номер (а), використовуючи таку формулу:

с = Ба мод p

с = 163 мод 17

с = 4096 мод 17

с = 16

Потім Боб виконує те, що є по суті тим же розрахунком, але з числом, яке йому надіслала Аліса (А), а також власний секретний номер (б):

с = Аб мод p

с = 136 мод 17

с = 4 826 809 мод 17

s = 16

Як бачимо, обидві сторони закінчилися однаковим результатом с, 16. Це спільний секрет, про який знають лише Аліса та Боб. Потім вони можуть використовувати це для встановлення ключа для симетричного шифрування, що дозволяє їм безпечно надсилати інформацію між собою таким чином, щоб лише вони мали доступ до неї.

Зауважимо, що хоча Б і с такі самі, як у наведеному вище прикладі, це лише збіг обставин, заснований на малій кількості, обраній для цієї ілюстрації. Зазвичай ці значення не були б однаковими в реальному здійсненні обміну ключами Діффі-Гелмана.

Незважаючи на те, що значна частина вищезазначених даних надсилається через канал у чіткому тексті (р, г, А і Б) і може бути прочитаний потенційними нападниками, спільним секретом (с) ніколи не передається. Зловмиснику не було б практично підрахувати загальну таємницю (с) або будь-який із секретних номерів (а і б) з інформації, що надсилається у чіткому тексті.

Звичайно, це передбачає, що обмін ключами Diffie-Hellman належним чином здійснено і використовується достатньо велика кількість. Поки ці положення дотримуються, обмін ключами Діффі-Гелмана вважається безпечним способом встановлення спільної таємниці, яка може бути використана для забезпечення майбутнього зв’язку.

Встановлення спільного ключа між кількома сторонами

Обмін ключами Diffie-Hellman також може використовуватися для встановлення спільного ключа з більшою кількістю учасників. Це працює таким же чином, за винятком подальших етапів обчислень, щоб кожна сторона мала додати свою секретну кількість і в кінцевому підсумку мати однаковий загальний секрет.

Як і в двосторонній версії обміну ключами Diffie-Hellman, деякі частини інформації надсилаються через незахищені канали, але недостатньо, щоб зловмисник міг обчислити загальну таємницю.

Чому безпечний обмін ключами Diffie-Hellman?

На математичному рівні обмін ключами Діффі-Гелмана покладається на односторонні функції як основу для його безпеки. Це розрахунки, які просто зробити одним способом, але набагато складніше обчислити у зворотному порядку.

Більш конкретно, вона спирається на проблему Діффі-Гелмана, яка передбачає, що за правильних параметрів неможливо розрахувати габ від окремих значень г, га і гб. Наразі загальновідомого способу легко знайти габ від інших значень, саме тому обмін ключами Діффі-Гелмана вважається безпечним, незважаючи на те, що зловмисники можуть перехоплювати значення p, г, А, і Б.

Аутентифікація & обмін ключами Діффі-Гелмана

У реальному світі обмін ключами Діффі-Гелмана рідко використовується сам по собі. Основна причина цього полягає в тому він не забезпечує аутентифікацію, що робить користувачів уразливими до атак “людина-в-середині”.

Ці атаки можуть мати місце, коли обмін ключами Діффі-Гелмана реалізується сам, оскільки у нього немає засобів перевірити, чи дійсно інша сторона у зв’язку є такою, якою вони кажуть. Без будь-якої форми аутентифікації, користувачі можуть фактично з’єднуватися з нападниками коли вони думають, що спілкуються з довіреною стороною.

З цієї причини обмін ключами Diffie-Hellman, як правило, здійснюється разом із деякими засобами аутентифікації. Це часто передбачає використання цифрових сертифікатів та алгоритму відкритого ключа, такого як RSA, для перевірки особи кожної сторони.

Варіації обміну ключами Діффі-Гелмана

Обмін ключами Diffie-Hellman може бути реалізований різними способами, і це також послужило основою для декількох інших алгоритмів. Деякі з цих реалізацій забезпечують авторизацію, в той час як інші мають різні криптографічні функції, такі як досконала секретність вперед.

Еліптично-крива Діффі-Гелман

Еліптична крива Діффі-Геллмана використовує перевагу алгебраїчної структури еліптичних кривих, щоб дозволити її реалізації досягти аналогічного рівня безпеки з меншим розміром ключа. 224-розрядний еліптичний кривий ключ забезпечує той самий рівень безпеки, що і 2048-розрядний ключ RSA. Це може зробити обмін більш ефективним і зменшити потреби в сховищі.

Окрім меншої довжини ключа та того, що він спирається на властивості еліптичних кривих, еліптична крива Діффі-Хеллмана діє аналогічно стандартному обміну ключами Diffie-Hellman.

TLS   

TLS – протокол, який використовується для забезпечення великої кількості Інтернету, може використовувати обмін Diffie-Hellman трьома різними способами: анонімним, статичним та ефемерним. На практиці слід реалізувати лише ефемерну Діффі-Гелман, оскільки інші варіанти мають проблеми із безпекою.

• Анонімний Діффі-Гелман – Ця версія обміну ключами Diffie-Hellman не використовує автентифікацію, що залишає її вразливою для атак людини в середині. Її не слід використовувати чи реалізовувати.
• Статична Діффі-Гелман – Статична Diffie-Hellman використовує сертифікати для аутентифікації сервера. Він не автентифікує клієнта за замовчуванням, а також не забезпечує передачу секретності.
• Ефемер Диффі-Гелман – Це вважається найбільш безпечною реалізацією, оскільки забезпечує ідеальну таємницю вперед. Зазвичай він поєднується з таким алгоритмом, як DSA або RSA для автентифікації однієї або обох сторін з’єднання. Ephemeral Diffie-Hellman використовує різні пари ключів при кожному запуску протоколу. Це надає з’єднанню ідеальну таємницю вперед, тому що навіть якщо ключ буде порушений у майбутньому, його не можна використовувати для розшифрування всіх попередніх повідомлень.

ElGamal

ElGamal – алгоритм відкритого ключа, побудований на основі обміну ключами Diffie-Hellman. Як і Діффі-Хеллман, він не містить положень про автентифікацію самостійно, і, як правило, поєднується з іншими механізмами для цієї мети.

ElGamal в основному використовувався в PGP, GNU Guard Guard та інших системах, оскільки його основний конкурент, RSA, був запатентований. Термін дії патенту RSA закінчився в 2000 році, що дозволило безперешкодно реалізовуватися після цієї дати. З того часу ElGamal не застосовується так часто.

ДПС

Протокол «Від станції до станції» (STS) також заснований на обміні ключів Diffie-Hellman. Це ще одна ключова схема домовленостей, проте вона забезпечує захист від атак людини в середині, а також ідеальну таємницю вперед.

Він вимагає, щоб обидві сторони у з’єднанні вже мали ключ, який використовується для аутентифікації кожної сторони. Якщо сторони вже не відомі один одному, то сертифікати можуть бути використані для підтвердження особи обох сторін.

Обмін ключами Діффі-Гелмана & RSA

Як ми обговорювали раніше, обмін ключами Diffie-Hellman часто реалізується поряд з RSA або іншими алгоритмами для забезпечення автентифікації для з’єднання. Якщо ви знайомі з RSA, можливо, вам цікаво чому б хтось не заважав використовувати обмін ключами Діффі-Гелмана, оскільки RSA дозволяє сторонам, які ніколи раніше не зустрічалися, безпечно спілкуватися.

RSA дозволяє своїм користувачам шифрувати повідомлення за допомогою відкритого ключа свого кореспондента, так що їх можна розшифрувати лише відповідним приватним ключем. Однак на практиці, RSA не використовується для шифрування всієї комунікації – це було б занадто неефективно.

Натомість RSA часто використовується лише як засіб аутентифікації обох сторін. Це робить це за допомогою цифрові сертифікати кожної сторони, які будуть перевірені сертифікаційним органом довести, що власник сертифікату справді є тим, про кого вони говорять, і що відкритий ключ у сертифікаті насправді належить їм.

Для взаємної аутентифікації, кожна сторона підпише повідомлення, використовуючи свій приватний ключ, а потім надішле його своєму партнеру по спілкуванню. Кожен одержувач може потім перевірити особу іншої сторони, перевіряючи підписані повідомлення проти відкритого ключа на цифровому сертифікаті партнера по зв’язку (див. вищезгадану статтю про RSA для отримання більш детальної інформації про те, як це працює, зокрема Підписання повідомлень розділ).

Тепер, коли обидві сторони пройшли автентифікацію, технічно можна продовжувати використовувати RSA для безпечного надсилання зашифрованих повідомлень між собою, однак це виявиться занадто неефективним.

Щоб подолати цю неефективність, багато протоколів безпеки використовують такий алгоритм, як обмін ключами Діффі-Гелмана, щоб створити загальний секрет, який можна використовувати для встановлення спільного симетричного ключа. Цей симетричний ключ потім використовується в алгоритмі симетричного ключа, наприклад AES, для шифрування даних що дві сторони мають намір надійно посилатись між собою.

Це може здатися складним і заплутаним процесом, але він закінчується набагато швидшим і менш вимогливим до ресурсів у порівнянні з використанням алгоритму відкритого ключа для всього обміну. Це відбувається тому Шифрування симетричним ключем на порядок ефективніше, ніж шифрування відкритим ключем.

Окрім неефективності, про яку ми нещодавно згадували, є й інші недоліки, які випливатимуть лише з використання RSA. RSA потребує прокладки, щоб зробити його надійним, тому додатковий алгоритм повинен бути належним чином реалізований поряд з ним, щоб зробити його безпечним.

RSA не забезпечує ідеальну таємницю вперед, або, що є ще одним недоліком порівняно з ефемерним обміном ключів Діффі-Гелмана. У сукупності ці причини є тим, що в багатьох ситуаціях найкраще застосовувати лише RSA у поєднанні з обміном ключів Diffie-Hellman.

Крім того, обмін ключами Diffie-Hellman може поєднуватися з таким алгоритмом, як Digital Digital Signature Standard (DSS), щоб забезпечити автентифікацію, обмін ключами, конфіденційність і перевірити цілісність даних. У такій ситуації RSA не потрібен для забезпечення з’єднання.

Питання безпеки обміну ключами Діффі-Гелмана

Захищеність обміну ключами Diffie-Hellman залежить від того, як він реалізований, а також від вибраних для нього цифр. Як ми говорили вище, він не має засобів аутентифікації іншої сторони сам по собі, але на практиці використовуються інші механізми для того, щоб інша сторона у зв’язку не була самозванець.

Параметри вибору числа

Якщо реальна реалізація обміну ключами Diffie-Hellman використовує цифри настільки ж невеликі, як у нашому прикладі, це зробило б процес обміну тривіальним для зловмисника. Але це не тільки величина чисел, які мають значення – номери також повинні бути досить випадковими. Якщо генератор випадкових чисел дає передбачуваний вихід, він може повністю підірвати безпеку обміну ключами Діффі-Гелмана.

Кількість p має бути 2048 біт для забезпечення безпеки. Основа, г, може бути порівняно невеликим числом, як 2, але це має виходити з наказу Г що має великий простий фактор

Атака Лоджам

Обмін ключами Diffie-Hellman був розроблений на основі важко розв’язаної дискретної логарифмічної проблеми. Найефективніший загальновідомий механізм пошуку рішення – алгоритм просіювання чисельного поля.

Можливості цього алгоритму були враховані при розробці обміну ключами Діффі-Гелмана. До 1992 року було відомо, що для даної групи, Г, три з чотирьох етапів алгоритму потенційно можна було б обчислити. Якщо цей прогрес був збережений, остаточний крок можна було б обчислити за порівняно короткий час.

Це було не надто стурбовано, поки не було зрозуміло, що значна частина інтернет-трафіку використовує ті самі групи, які мають 1024 біт або менше. У 2015 році академічна команда здійснила обчислення найпоширенішого 512-бітного прем’єра, використовуваного обміном ключами Diffie-Hellman в TLS.

Вони також змогли знизити 80% серверів TLS, які підтримують DHE-EXPORT, щоб вони прийняли 512-бітний експортний клас обміну Diffie-Hellman для з’єднання. Це означає що кожен з цих серверів вразливий до атаки з боку супротивника, який добре використовує ресурси.

Дослідники продовжували екстраполювати свої результати, підрахувавши, що національна держава може зламати 1024-бітну прем’єр-мінімум. Розбивши єдиний 1024-розрядний прем’єр-міністр, академічна команда підрахувала, що противник може контролювати 18% мільйона найпопулярніших веб-сайтів HTTPS.

Вони продовжували говорити, що другий прайм дозволить противнику розшифрувати з’єднання 66% серверів VPN та 26% серверів SSH. Пізніше у звіті вчені припустили, що АНБ вже може мати ці можливості.

“Уважне читання опублікованих витоків НСА показує, що напади агентства на VPN узгоджуються з тим, що досягли такого перерви”.

Незважаючи на цю вразливість, обмін ключами Diffie-Hellman все ще може бути безпечним, якщо він правильно виконаний. Поки використовується 2048-бітний ключ, атака Logjam не буде працювати. Оновлені браузери також захищені від цієї атаки.

Чи безпечний обмін ключами Diffie-Hellman?

Хоча обмін ключами Diffie-Hellman може здатися складним, він є основою надійного обміну даними в Інтернеті. Поки він реалізований поряд із відповідним методом аутентифікації та чисельністю вибрано належним чином, він не вважається вразливим для атаки.

Обмін ключами Діффі-Гелмана був інноваційним методом допомоги двом невідомим сторонам в безпечній комунікації, коли вона була розроблена в 1970-х. Зараз ми впроваджуємо новіші версії з більшими клавішами для захисту від сучасних технологій сам протокол виглядає так, що він буде надалі захищеним до приходу квантових обчислень і передові атаки, які будуть пов’язані з цим.

Бізнес-технології в галузі кібербезпеки автор: TheDigitalArtist, ліцензований відповідно до CC0