Mã hóa RSA là gì và nó hoạt động như thế nào?

Mã hóa RSA là một hệ thống giải quyết những gì từng là một trong những vấn đề lớn nhất trong ngành mật mã: Làm thế nào bạn có thể gửi cho ai đó một tin nhắn được mã hóa mà không có cơ hội chia sẻ mã trước đó với họ?

Bài viết này sẽ dạy cho bạn mọi thứ bạn cần biết về cách mã hóa RSA được phát triển, làm thế nào nó hoạt động, toán học đằng sau nó, nó dùng để làm gì cũng như một số vấn đề bảo mật lớn nhất mà nó phải đối mặt. Tìm hiểu về RSA sẽ cung cấp cho bạn một số kiến ​​thức nền tảng giúp bạn hiểu được có bao nhiêu phần trong cuộc sống trực tuyến của chúng tôi được giữ an toàn.

Mã hóa RSA là gì?

Hãy nói với bạn rằng bạn muốn nói với bạn của bạn một bí mật. Nếu bạn ngay bên cạnh họ, bạn có thể thì thầm điều đó. Nếu bạn ở hai phía đối diện đất nước, điều đó rõ ràng đã thắng công việc của Keith. Bạn có thể viết nó xuống và gửi thư cho họ, hoặc sử dụng điện thoại, nhưng mỗi kênh truyền thông này không an toàn và bất cứ ai có động lực đủ mạnh có thể dễ dàng chặn tin nhắn.

Nếu bí mật đó đủ quan trọng, bạn sẽ có nguy cơ viết nó xuống các gián điệp bình thường hoặc một nhân viên bưu chính lừa đảo có thể đang xem qua thư của bạn. Tương tự như vậy, ai đó có thể nhấn vào điện thoại của bạn mà bạn không biết và ghi lại mọi cuộc gọi bạn thực hiện.

Một giải pháp để ngăn chặn kẻ nghe trộm truy cập nội dung tin nhắn là mã hóa nó. Điều này về cơ bản có nghĩa là thêm một mã vào tin nhắn mà thay đổi nó thành một mớ hỗn độn. Nếu mã của bạn đủ phức tạp, thì những người duy nhất có thể truy cập thư gốc là những người có quyền truy cập vào mã.

Nếu bạn đã có cơ hội chia sẻ mã với bạn bè của mình trước đó, thì một trong hai bạn có thể gửi tin nhắn được mã hóa bất cứ lúc nào, biết rằng hai bạn là những người duy nhất có khả năng đọc nội dung tin nhắn. Nhưng chuyện gì sẽ xảy ra nếu bạn không có cơ hội chia sẻ mã trước đó?

Đây là một trong những vấn đề cơ bản của mật mã học, đã được giải quyết bởi lược đồ mã hóa khóa công khai (còn được gọi là mã hóa bất đối xứng) như RSA.

Theo mã hóa RSA, tin nhắn được mã hóa bằng mã gọi là khóa công khai, có thể được chia sẻ một cách cởi mở. Do một số tính chất toán học riêng biệt của thuật toán RSA, một khi tin nhắn đã được mã hóa bằng khóa chung, nó chỉ có thể được giải mã bằng một khóa khác, được gọi là khóa riêng. Mỗi người dùng RSA có một cặp khóa bao gồm khóa chung và khóa riêng của họ. Như tên cho thấy, khóa riêng phải được giữ bí mật.

Các lược đồ mã hóa khóa công khai khác với Mã hóa khóa đối xứng, trong đó cả quá trình mã hóa và giải mã đều sử dụng cùng một khóa riêng. Những khác biệt này làm cho mã hóa khóa công khai như RSA trở nên hữu ích để liên lạc trong các tình huống không có cơ hội phân phối khóa an toàn trước đó.

Các thuật toán khóa đối xứng có các ứng dụng riêng của chúng, chẳng hạn như mã hóa dữ liệu cho sử dụng cá nhân hoặc khi có các kênh bảo mật mà các khóa riêng có thể được chia sẻ qua.

Xem thêm: Mật mã khóa công khai

Mã hóa RSA được sử dụng ở đâu?

Mã hóa RSA thường được sử dụng trong kết hợp với các chương trình mã hóa khác, hoặc là chữ ký số có thể chứng minh tính xác thực và tính toàn vẹn của tin nhắn. Nó thường được sử dụng để mã hóa toàn bộ tin nhắn hoặc tập tin, vì nó kém hiệu quả và tốn nhiều tài nguyên hơn so với mã hóa khóa đối xứng.

Để làm cho mọi thứ hiệu quả hơn, một tệp thường sẽ được mã hóa bằng thuật toán khóa đối xứng và sau đó khóa đối xứng sẽ được mã hóa bằng mã hóa RSA. Theo quy trình này, chỉ có một thực thể có quyền truy cập vào khóa riêng RSA mới có thể giải mã khóa đối xứng.

Không thể truy cập khóa đối xứng, tập tin gốc có thể được giải mã. Phương pháp này có thể được sử dụng để giữ an toàn cho tin nhắn và tệp mà không mất quá nhiều thời gian hoặc tiêu tốn quá nhiều tài nguyên tính toán.

Mã hóa RSA có thể được sử dụng trong một số hệ thống khác nhau. Nó có thể được triển khai trong OpenSSL, wolfCrypt, cryptlib và một số thư viện mã hóa khác.

Là một trong những chương trình mã hóa khóa công khai được sử dụng rộng rãi đầu tiên, RSA đã đặt nền móng cho phần lớn các liên lạc an toàn của chúng tôi. Đó là theo truyền thống được sử dụng trong TLS và cũng là thuật toán ban đầu được sử dụng trong mã hóa PGP. RSA vẫn được thấy trong một loạt các trình duyệt web, email, VPN, trò chuyện và các kênh liên lạc khác.

RSA cũng thường được sử dụng để tạo kết nối an toàn giữa máy khách VPN và máy chủ VPN. Trong các giao thức như OpenVPN, bắt tay TLS có thể sử dụng thuật toán RSA để trao đổi khóa và thiết lập kênh an toàn.

Nền tảng của mã hóa RSA

Như chúng tôi đã đề cập ở đầu bài viết này, trước khi mã hóa khóa công khai, việc giao tiếp an toàn là một thách thức nếu không có cơ hội trao đổi khóa an toàn trước đó. Nếu không có cơ hội chia sẻ mã trước thời hạn hoặc kênh an toàn mà qua đó các khóa có thể được phân phối, không có cách nào để liên lạc mà không có mối đe dọa của kẻ thù có thể chặn và truy cập nội dung tin nhắn.

Cho đến những năm 1970, mọi thứ thực sự bắt đầu thay đổi. Sự phát triển lớn đầu tiên hướng tới cái mà chúng ta gọi là mật mã khóa công khai đã được James H. Ellis xuất bản vào đầu thập kỷ này. Ellis không thể tìm thấy một cách để thực hiện công việc của mình, nhưng nó đã được mở rộng bởi đồng nghiệp Clifford Cocks để trở thành những gì chúng ta biết bây giờ là Mã hóa RSA.

Phần cuối cùng của câu đố là cái mà bây giờ chúng ta gọi là Trao đổi khóa Diffie-Hellman. Malcolm J. Williamson, một đồng nghiệp khác, đã tìm ra một kế hoạch cho phép hai bên chia sẻ khóa mã hóa, ngay cả khi kênh đang bị đối thủ theo dõi.

Tất cả các công việc này được thực hiện tại cơ quan tình báo Vương quốc Anh, Trụ sở Truyền thông Chính phủ (GCHQ), trong đó giữ cho khám phá được phân loại. Một phần do những hạn chế về công nghệ, GCHQ không thể thấy việc sử dụng mật mã khóa công khai vào thời điểm đó, vì vậy sự phát triển nằm im trên kệ thu thập bụi. Cho đến năm 1997, công việc đã được giải mật và các nhà phát minh ban đầu của RSA đã được công nhận.

Vài năm sau, các khái niệm tương tự đã bắt đầu phát triển trong lĩnh vực công cộng. Ralph Merkle đã tạo ra một hình thức ban đầu của mật mã khóa công khai, đã ảnh hưởng đến Whitfield Diffie và Martin Hellman trong thiết kế trao đổi khóa Diffie-Hellman.

Ý tưởng của Diffie và Hellman, đã thiếu một khía cạnh quan trọng giúp công việc của họ trở thành nền tảng của mật mã khóa công khai. Đây là một chức năng một chiều sẽ khó đảo. Năm 1977, Ron Rivest, Adi Shamir và Leonard Adeld, tên cuối cùng tạo thành từ viết tắt RSA, đã đưa ra một giải pháp sau một năm lao động về vấn đề này.

Các học giả có trụ sở tại MIT đã tạo ra bước đột phá sau bữa tiệc Vượt qua vào năm 1977. Sau một đêm uống rượu, Rivest về nhà, nhưng thay vì ngủ, anh ta đã dành một buổi tối sốt sắng viết một bài báo chính thức hóa ý tưởng của mình cho chức năng một chiều cần thiết.

Ý tưởng đã được MIT cấp bằng sáng chế vào năm 1983, nhưng đến tận những ngày đầu của Internet, thuật toán RSA bắt đầu thấy việc áp dụng rộng rãi như một công cụ bảo mật quan trọng.

Mã hóa RSA hoạt động như thế nào?

Sau đây sẽ là một chút đơn giản hóa, bởi vì quá nhiều độc giả có thể đã bị sẹo bởi giáo viên toán trung học của họ. Để giữ cho toán học không bị quá tầm tay, chúng ta sẽ đơn giản hóa một số khái niệm và sử dụng số lượng nhỏ hơn nhiều. Trong thực tế, mã hóa RSA sử dụng các số nguyên tố có độ lớn lớn hơn nhiều và có một vài phức tạp khác.

Có một số khái niệm khác nhau mà bạn sẽ phải suy nghĩ kỹ trước khi chúng tôi có thể giải thích làm thế nào tất cả khớp với nhau. Bao gồm các Các hàm bẫy, tạo các số nguyên tố, hàm tổng số của Carmichael và các quy trình riêng biệt liên quan đến tính toán các khóa công khai và riêng tư được sử dụng trong quá trình mã hóa và giải mã.

Chức năng cửa bẫy

Mã hóa RSA hoạt động với tiền đề là thuật toán dễ dàng tính toán theo một hướng, nhưng gần như không thể đảo ngược. Ví dụ, nếu bạn được thông báo rằng 701.111 là sản phẩm của hai số nguyên tố, bạn có thể tìm ra hai số đó là gì không?

Ngay cả với một máy tính hoặc máy tính, hầu hết chúng ta đều không có ý tưởng về việc bắt đầu từ đâu, chứ đừng nói đến việc có thể tìm ra câu trả lời. Nhưng nếu chúng ta lật mọi thứ xung quanh, nó sẽ trở nên dễ dàng hơn nhiều. Những gì kết quả của:

907 x 773

Nếu bạn đã đủ chán, bạn sẽ có thể rút điện thoại ra hoặc có thể tính toán nó trong đầu để khám phá ra rằng câu trả lời là 701.111 đã đề cập trước đó. 907 và 773 này là các số nguyên tố trả lời câu hỏi đầu tiên của chúng tôi, cho chúng ta thấy rằng các phương trình nhất định có thể dễ dàng tìm ra một cách, nhưng dường như không thể đảo ngược.

Một khía cạnh thú vị khác của phương trình này là rất đơn giản để tìm ra một trong những số nguyên tố nếu bạn đã có một số khác, cũng như sản phẩm. Nếu bạn được thông báo rằng 701.111 là kết quả của 907 nhân với một số nguyên tố khác, bạn có thể tìm ra số nguyên tố khác với phương trình sau:

701.111 907 = 773

Vì mối quan hệ giữa các số này rất đơn giản để tính theo một hướng, nhưng cực kỳ khó đảo ngược, nên phương trình được gọi là chức năng cửa bẫy. Xin lưu ý rằng trong khi ví dụ trên khó có thể hiểu được, máy tính có thể thực hiện thao tác trong một khoảng thời gian không đáng kể.

Bởi vì điều này, RSA sử dụng số lượng lớn hơn nhiều. Kích thước của các số nguyên tố trong triển khai RSA thực tế khác nhau, nhưng trong RSA 2048 bit, chúng sẽ kết hợp với nhau để tạo ra các khóa dài 617 chữ số. Để giúp bạn hình dung ra nó, một phím sẽ là một số có kích thước này:

99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

Tạo số nguyên tố

Các chức năng cửa bẫy được đề cập ở trên tạo cơ sở cho cách thức hoạt động của các chương trình mã hóa khóa công khai và khóa riêng. Các thuộc tính của chúng cho phép các khóa chung được chia sẻ mà không gây nguy hiểm cho tin nhắn hoặc tiết lộ khóa riêng. Họ cũng cho phép dữ liệu được mã hóa bằng một khóa theo cách chỉ có thể được giải mã bằng khóa khác từ cặp.

Bước đầu tiên để mã hóa tin nhắn bằng RSA là tạo các phím. Để làm điều này, chúng ta cần hai số nguyên tố (p và q) được chọn với một bài kiểm tra nguyên thủy. Kiểm tra tính nguyên thủy là một thuật toán tìm hiệu quả các số nguyên tố, chẳng hạn như kiểm tra tính nguyên thủy Rabin-Miller.

Các số nguyên tố trong RSA cần phải rất lớn và cũng tương đối xa nhau. Các số nhỏ hoặc gần nhau dễ bị bẻ khóa hơn nhiều. Mặc dù vậy, ví dụ của chúng tôi sẽ sử dụng các số nhỏ hơn để làm cho mọi thứ dễ theo dõi và tính toán hơn.

Hãy nói rằng bài kiểm tra nguyên thủy cho chúng ta các số nguyên tố mà chúng ta đã sử dụng ở trên, 907 và 773. Bước tiếp theo là khám phá mô đun (n), sử dụng công thức sau:

n = = p x q

Ở đâu p = 907 và q = 773

Vì thế:

n = 907 x 773

n = 701.111

Hàm toàn phần của Carmichael

Một khi chúng ta có n, chúng tôi sử dụng Hàm tổng số của Carmichael từ:

    λ(n) = = lcm (p – 1, q – 1)

Nếu nó đã được một lúc kể từ khi bạn tấn công vào sách giáo khoa toán học, những điều trên có thể trông hơi đáng sợ. Bạn có thể bỏ qua phần này và chỉ tin tưởng rằng toán học hoạt động, nếu không hãy gắn bó với chúng tôi để có thêm một vài tính toán. Mọi thứ sẽ được giải thích chi tiết nhất có thể để giúp bạn hiểu được những điều cơ bản.

Dành cho những ai nhận biết, λ (n) đại diện cho Carmichael từ toàn bộ cho n, trong khi lcm có nghĩa là bội số chung thấp nhất, đó là con số thấp nhất mà cả hai p và q có thể chia thành. Có một vài cách khác nhau để tìm ra điều này, nhưng cách dễ nhất là tin tưởng một máy tính trực tuyến để thực hiện phương trình cho bạn. Vì vậy, hãy để Lừa đưa số của chúng tôi vào phương trình:

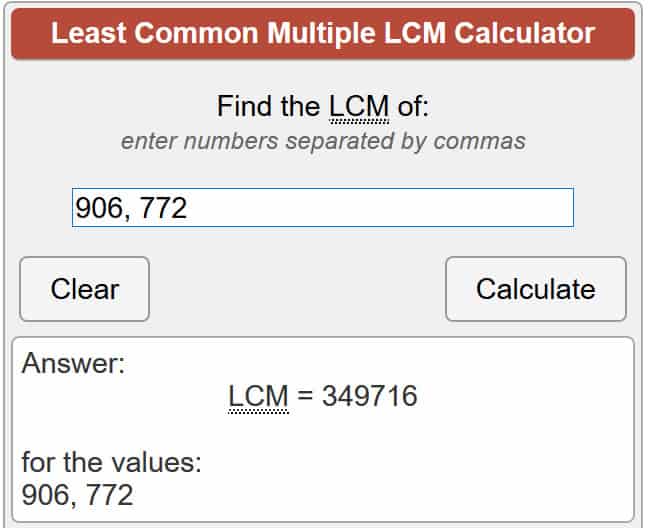
    λ(701.111) = = lcm (907 – 1, 773 – 1)

    λ(701.111) = = lcm (906, 772)

   Sử dụng máy tính được liên kết ở trên, điều này cho chúng ta:

    λ(701.111) = 349,716

Tạo khóa công khai

Bây giờ chúng ta đã có được số nguyên tố của Carmichael thời gian để tìm ra khóa công khai của chúng tôi. Theo RSA, khóa công khai được tạo thành từ một số nguyên tố e, cũng như n. Con số e có thể là bất cứ thứ gì giữa 1 và giá trị cho λ(n), trong ví dụ của chúng tôi là 349,716.

Vì khóa công khai được chia sẻ công khai, nên nó không quá quan trọng đối với e là một số ngẫu nhiên. Trong thực tế, e thường được đặt tại 65,537, bởi vì khi số lượng lớn hơn nhiều được chọn ngẫu nhiên, nó làm cho việc mã hóa kém hiệu quả hơn nhiều. Đối với ví dụ ngày hôm nay, chúng tôi sẽ giữ các số nhỏ để tính toán hiệu quả. Hãy cùng nói nào:

e = 11

Dữ liệu được mã hóa cuối cùng của chúng tôi được gọi là bản mã (c). Chúng tôi lấy nó từ tin nhắn văn bản gốc của chúng tôi (m), bằng cách áp dụng khóa chung với công thức sau:

c = = me mod n

Chúng tôi đã đưa ra e và chúng ta biết n cũng. Điều duy nhất chúng ta cần giải thích là mod. Nó khác một chút về chiều sâu của bài viết này, nhưng nó đề cập đến một hoạt động modulo, về cơ bản có nghĩa là phần còn lại còn lại khi bạn chia một bên cho bên kia. Ví dụ:

10 mod 3 = 1

Điều này là do 3 đi vào 10 ba lần, với phần còn lại là 1.

Quay lại phương trình của chúng tôi. Để giữ cho mọi thứ đơn giản, hãy để nói rằng thông điệp (m) mà chúng tôi muốn mã hóa và giữ bí mật chỉ là một số duy nhất, 4. Hãy để cắm tất cả mọi thứ vào:

c = = me mod n

c = 411 mod 701.111

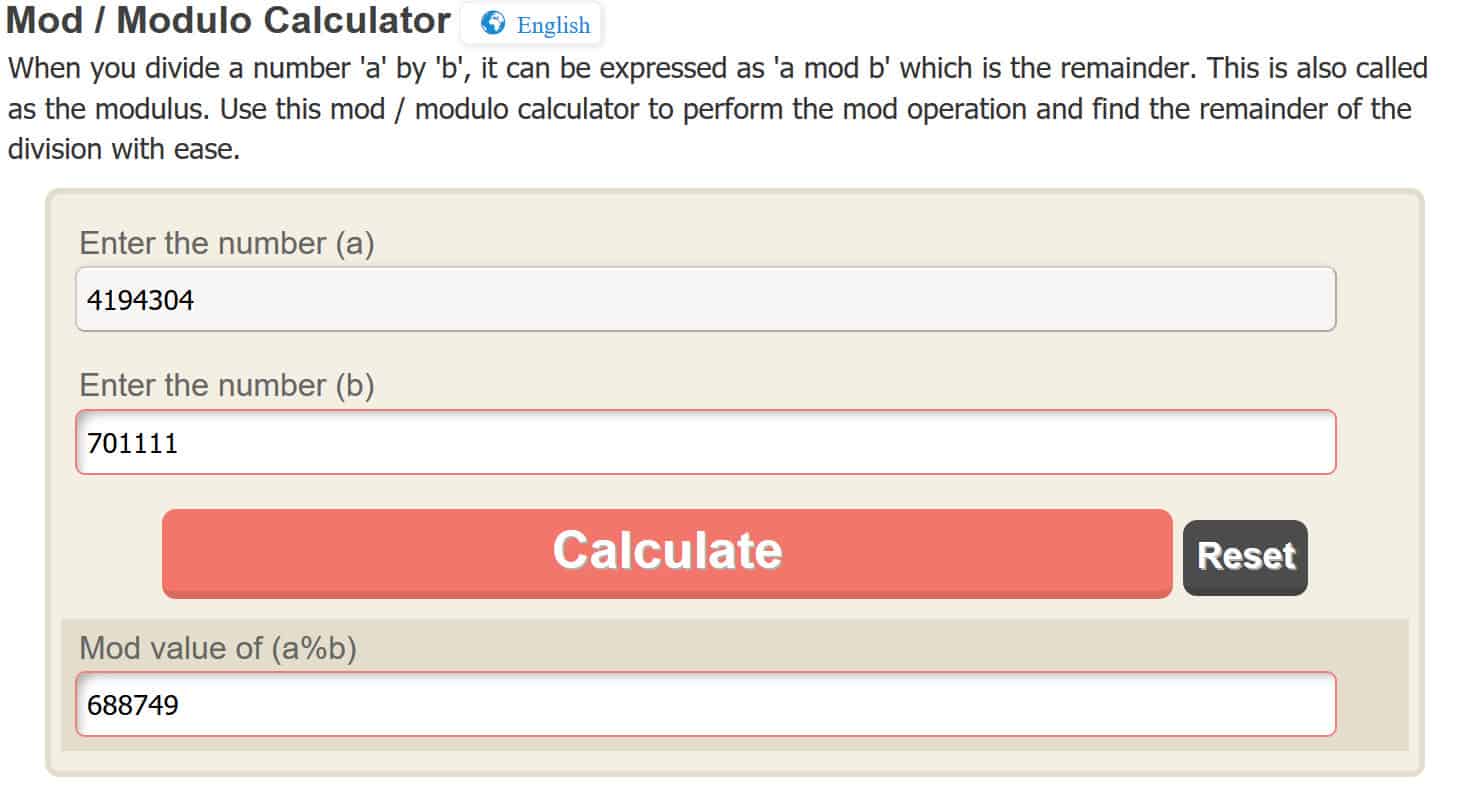
c = 4.194.304 mod 701.111

Một lần nữa, để làm cho hoạt động modulo thật dễ dàng, chúng tôi sẽ sử dụng một máy tính trực tuyến, nhưng bạn có thể tự mình tìm ra nó. Bằng cách nhập 4.194.304 vào máy tính trực tuyến, nó cho chúng ta:

c = 688,749

Do đó, khi chúng tôi sử dụng RSA để mã hóa tin nhắn của mình, 4, với khóa công khai của chúng tôi, nó cung cấp cho chúng tôi bản mã của 688.749. Các bước trước có vẻ hơi nặng về toán học, nhưng điều quan trọng là phải nhắc lại những gì đã xảy ra.

Chúng tôi đã có một tin nhắn của 4, mà chúng tôi muốn giữ bí mật. Chúng tôi đã áp dụng một khóa công khai cho nó, nó đã cho chúng tôi kết quả được mã hóa của 688.749. Bây giờ nó được mã hóa, chúng tôi có thể gửi số 688.749 một cách an toàn cho chủ sở hữu của cặp khóa. Họ là người duy nhất có thể giải mã nó bằng khóa riêng của họ. Khi họ giải mã nó, họ sẽ thấy thông điệp mà chúng tôi thực sự đang gửi, 4.

Tạo khóa riêng

Trong mã hóa RSA, một khi dữ liệu hoặc tin nhắn đã được chuyển thành bản mã bằng khóa chung, nó chỉ có thể được giải mã bằng khóa riêng từ cùng một cặp khóa. Khóa riêng bao gồm d và n. Chúng tôi đã biết n, và phương trình sau đây được sử dụng để tìm d:

d = 1 /e λ(n)

bên trong Tạo khóa công khai phần trên, chúng tôi đã quyết định rằng trong ví dụ của chúng tôi, e sẽ bằng 11. Tương tự, chúng ta biết rằng λ(n) bằng 349,716 từ công việc trước đây của chúng tôi Hàm toàn phần của Carmichael. Mọi thứ trở nên phức tạp hơn một chút khi chúng ta bắt gặp phần này của công thức:

1 /e mod

Phương trình này có thể trông giống như nó yêu cầu bạn chia 1 cho 11, nhưng điều đó không đúng. Thay vào đó, điều này chỉ tượng trưng cho việc chúng ta cần tính toán mô đun nghịch đảo của e (trong trường hợp này là 11) và λ(n) (trong trường hợp này là 349,716).

Điều này về cơ bản có nghĩa là thay vì thực hiện thao tác modulo tiêu chuẩn, chúng tôi sẽ sử dụng nghịch đảo thay thế. Điều này thường được tìm thấy với Thuật toán Euclide mở rộng, nhưng nó có một chút nằm ngoài phạm vi của bài viết này, vì vậy chúng tôi sẽ chỉ gian lận và sử dụng một máy tính trực tuyến thay thế. Bây giờ chúng tôi đã hiểu tất cả mọi thứ mà Vĩ đang diễn ra, hãy để Lít cắm thông tin của chúng tôi vào công thức:

d = 1 /11 mod 349,716

Để thực hiện thao tác này, chỉ cần nhập 11 (hoặc bất kỳ giá trị nào bạn có thể có cho e nếu bạn đang cố gắng điều này với ví dụ của riêng bạn) nơi nó nói Số nguyên và 349.716 (hoặc bất kỳ giá trị nào bạn có thể có λ(n) nếu bạn đang cố gắng điều này với ví dụ của riêng bạn) nơi nó nói Modulo trong máy tính trực tuyến đã được liên kết ở trên. Nếu bạn đã thực hiện đúng, bạn sẽ nhận được một kết quả trong đó:

d = 254, 339

Bây giờ chúng ta có giá trị cho d, chúng tôi có thể giải mã các tin nhắn được mã hóa bằng khóa chung của chúng tôi bằng công thức sau:

m = = cd mod n

Bây giờ chúng ta có thể quay lại bản mã mà chúng ta đã mã hóa theo Tạo khóa riêng phần. Khi chúng tôi mã hóa tin nhắn bằng khóa chung, nó đã cho chúng tôi một giá trị cho c 688.749. Từ trên cao, chúng ta biết rằng d bằng 254.339. Chúng tôi cũng biết rằng n bằng 701.111. Điều này cho chúng ta:

m = 688,749254.339 mod 701.111.

Như bạn có thể nhận thấy, cố gắng đưa một con số đến sức mạnh thứ 254.339 có thể là một chút ít đối với hầu hết các máy tính bình thường. Thay vào đó, chúng tôi sẽ sử dụng máy tính giải mã RSA trực tuyến. Nếu bạn muốn sử dụng một phương pháp khác, bạn sẽ áp dụng các quyền hạn như bình thường và thực hiện thao tác mô đun theo cách tương tự như chúng ta đã làm trong Tạo khóa công khai phần.

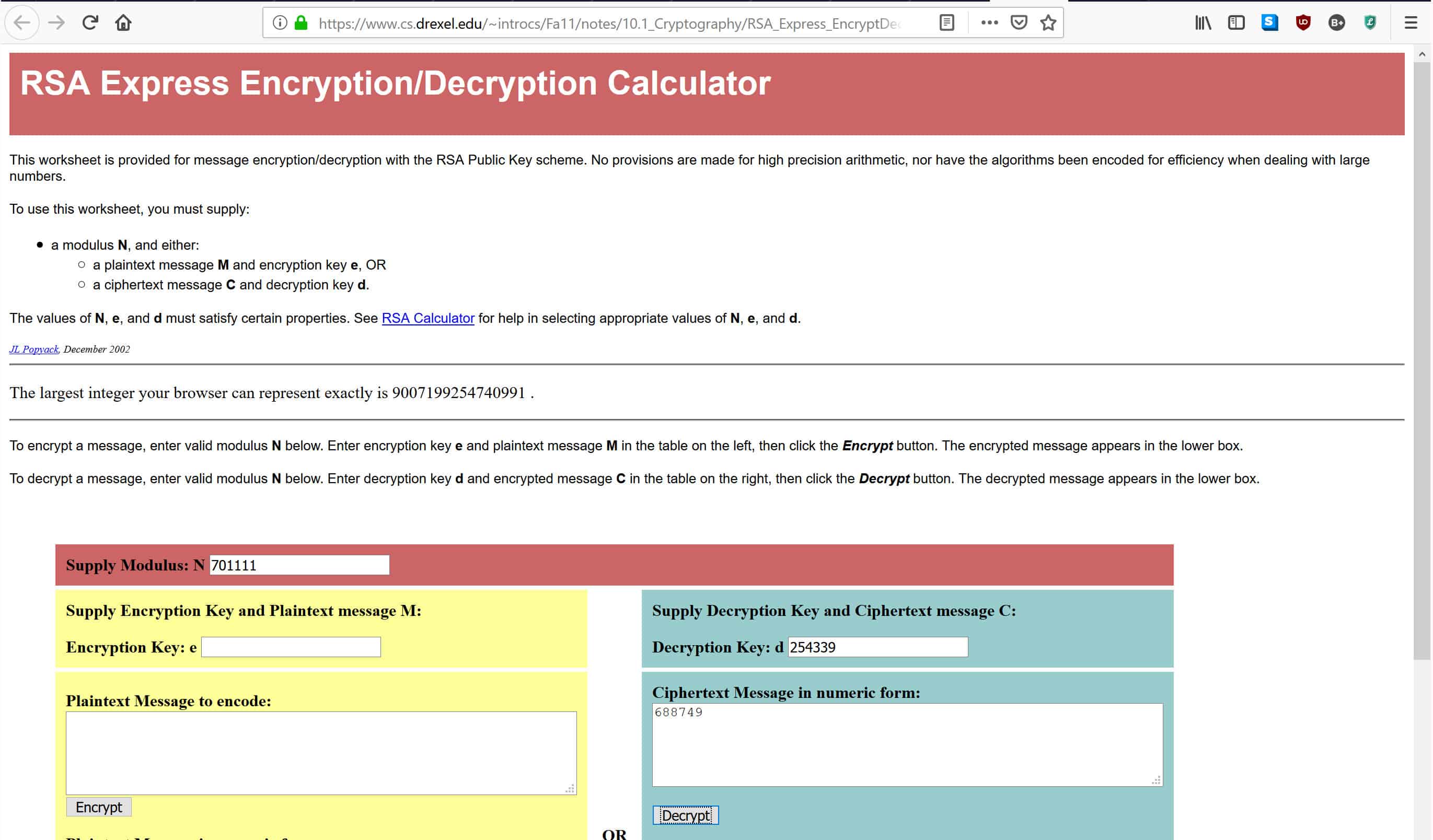
Trong máy tính được liên kết ở trên, nhập 701.111 vào đó nói Mô-đun cung ứng: N, 254.399 nơi nó nói Khóa giải mã: D, và 688.749 nơi nó nói Tin nhắn văn bản dưới dạng số, như hình dưới đây:

Khi bạn đã nhập dữ liệu, nhấn Giải mã, sẽ đưa các số thông qua công thức giải mã được liệt kê ở trên. Điều này sẽ cung cấp cho bạn thông điệp ban đầu trong hộp bên dưới. Nếu bạn đã làm mọi thứ chính xác, bạn sẽ nhận được câu trả lời về 4, đó là thông điệp ban đầu mà chúng tôi đã mã hóa bằng khóa chung của chúng tôi.

Cách mã hóa RSA hoạt động trong thực tế

Các phần trên sẽ cung cấp cho bạn một nắm bắt hợp lý về cách toán học đằng sau mã hóa khóa công khai hoạt động. Nó có thể hơi khó hiểu, nhưng ngay cả những người đã không hiểu được sự phức tạp của các phương trình có thể hy vọng lấy đi một số thông tin quan trọng về quy trình.

Trong các bước được liệt kê ở trên, chúng tôi đã chỉ ra cách hai thực thể có thể giao tiếp an toàn mà không cần chia sẻ mã trước đó. Đầu tiên, mỗi người cần thiết lập các cặp khóa riêng của họ và chia sẻ khóa chung với nhau. Hai thực thể cần giữ bí mật khóa riêng của họ để giữ liên lạc của họ được an toàn.

Khi người gửi có khóa chung của người nhận, họ có thể sử dụng nó để mã hóa dữ liệu mà họ muốn giữ an toàn. Khi nó đã được mã hóa bằng khóa chung, nó chỉ có thể được giải mã bằng khóa riêng từ cùng một cặp khóa. Ngay cả khóa công khai tương tự cũng có thể được sử dụng để giải mã dữ liệu. Điều này là do các thuộc tính của chức năng cửa bẫy mà chúng tôi đã đề cập ở trên.

Khi người nhận nhận được tin nhắn được mã hóa, họ sử dụng khóa riêng để truy cập dữ liệu. Nếu người nhận muốn trả lại thông tin liên lạc một cách an toàn, sau đó họ có thể mã hóa tin nhắn của mình bằng khóa chung của bên mà họ đang liên lạc. Một lần nữa, một khi nó đã được mã hóa bằng khóa chung, cách duy nhất mà thông tin có thể được truy cập là thông qua khóa riêng phù hợp.

Theo cách này, mã hóa RSA có thể được sử dụng bởi các bên chưa biết trước đây để gửi dữ liệu an toàn giữa họ. Các phần quan trọng của các kênh truyền thông mà chúng tôi sử dụng trong cuộc sống trực tuyến của chúng tôi đã được xây dựng từ nền tảng này.

Làm thế nào các tin nhắn phức tạp hơn được mã hóa với RSA?

Trong ví dụ của chúng tôi, chúng tôi đã đơn giản hóa mọi thứ rất nhiều để dễ hiểu hơn, đó là lý do tại sao chúng tôi chỉ mã hóa một tin nhắn của 4 4. Có thể mã hóa số 4 không có vẻ như đặc biệt hữu ích, vì vậy bạn có thể tự hỏi làm thế nào bạn có thể mã hóa một tập hợp dữ liệu phức tạp hơn, chẳng hạn như khóa đối xứng (là cách sử dụng phổ biến nhất của RSA) hoặc thậm chí là một tin nhắn.

Một số người có thể lúng túng khi biết một khóa như từ n38cb29fkbjh138g7fqijnf3kaj84f8b9f, hay một tin nhắn như của ông mua cho tôi một chiếc bánh sandwich có thể được mã hóa bằng thuật toán như RSA. Thực tế là tất cả thông tin mà máy tính của chúng tôi xử lý được lưu trữ ở dạng nhị phân (1 và 0) và chúng tôi sử dụng các tiêu chuẩn mã hóa như ASCII hoặc Unicode đại diện cho chúng theo cách mà con người có thể hiểu (chữ cái).

Điều này có nghĩa rằng các khóa như Khác n38cb29fkbjh138g7fqijnf3kaj84f8b9f Trò chơi và tin nhắn như Chuyện mua cho tôi một chiếc bánh sandwich đã tồn tại dưới dạng số, có thể dễ dàng được tính toán trong thuật toán RSA. Các số mà chúng được đại diện bởi chúng lớn hơn và khó quản lý hơn, đó là lý do tại sao chúng tôi thích xử lý các ký tự chữ và số hơn là một mớ hỗn độn của nhị phân.

Nếu bạn muốn mã hóa khóa phiên dài hơn hoặc tin nhắn phức tạp hơn với RSA, đơn giản là nó sẽ liên quan đến số lượng lớn hơn nhiều.

Đệm

Khi RSA được thực thi, nó sử dụng một cái gì đó gọi là đệm để giúp ngăn chặn một số cuộc tấn công. Để giải thích cách thức hoạt động của nó, chúng tôi sẽ bắt đầu với một ví dụ. Hãy nói rằng bạn đang gửi một tin nhắn được mã hóa cho một người bạn:

Karen thân mến,

    Tôi hy vọng bạn khỏe. Ngày mai chúng ta vẫn ăn tối chứ?

    Trân trọng,

    James

Hãy để nói rằng bạn đã mã hóa tin nhắn một cách đơn giản thay đổi từng chữ cái theo sau trong bảng chữ cái. Điều này sẽ thay đổi thông báo thành:

Efbs Lbsfo,

    J ipqf zpv bsf xfmm. Bsf xf tujmm ibwjoh ejoofs upnpsspx?

    Zpvst tjodfsfmz,

    Kbnft

Nếu kẻ thù của bạn chặn lá thư này, có một mẹo mà họ có thể sử dụng để thử và bẻ khóa mã. Họ có thể nhìn vào định dạng thư của bạn và cố gắng đoán xem tin nhắn có thể nói gì. Họ biết rằng mọi người thường bắt đầu những lá thư của họ bằng cách sử dụng Hi Hi,, Xin chào, Đây là một số quy ước khác..

Nếu họ cố gắng áp dụng từ Hi Hi hay hoặc Hello Hello làm từ đầu tiên, họ sẽ thấy rằng nó sẽ phù hợp với số lượng ký tự. Sau đó, họ có thể dùng thử Nó phù hợp, nhưng điều đó không nhất thiết có nghĩa là bất cứ điều gì. Những kẻ tấn công sẽ thử nó và xem nó dẫn chúng đến đâu. Vì vậy, họ sẽ thay đổi các chữ cái, và một phần mềm, với sự khác biệt. Điều này sẽ cung cấp cho họ:

Gửi Laseo,

    J ipqe zpv đang xem. Là xe tujmm iawjoh djooes upnpsspx?

    Zpvrt tjoderemz,

    Kanet

Trông vẫn khá khó hiểu, vì vậy những kẻ tấn công có thể thử nhìn vào một số quy ước khác, giống như cách chúng tôi kết thúc thư của chúng tôi. Cuối cùng, mọi người thường thêm vào các loại từ Từ hay các loại khác về vấn đề này, nhưng cả hai đều không phù hợp với định dạng này. Thay vào đó, những kẻ tấn công có thể dùng thử Trân Trân và thay thế các chữ cái khác để xem chúng lấy chúng ở đâu. Bằng cách thay đổi cách ăn vặt, thời trang, sự kiện, sự kiện, sự kiện lần lượt, những người khác, họ có thể nhận được:

Lasen thân mến,

    Tôi ioqe bạn là xell. Là xe tuill iawinh dinnes uonossox?

    Trân trọng,

    Kanet

Sau sửa đổi đó, có vẻ như những kẻ tấn công đang bắt đầu đi đến một nơi nào đó. Họ đã tìm thấy các từ trong đó là tôi, và bạn là người khác, ngoài những từ tạo nên những dự đoán ban đầu của họ.

Nhìn thấy các từ theo đúng thứ tự ngữ pháp, những kẻ tấn công có thể khá tự tin rằng chúng đang đi đúng hướng. Đến bây giờ, có lẽ họ cũng đã nhận ra rằng mã liên quan đến mỗi chữ cái được thay đổi thành chữ cái theo sau trong bảng chữ cái. Một khi họ nhận ra điều này, nó dễ dàng dịch phần còn lại và đọc tin nhắn gốc.

Ví dụ trên chỉ là một mã đơn giản, nhưng như bạn có thể thấy, cấu trúc của một thông điệp có thể cung cấp cho kẻ tấn công manh mối về nội dung của nó. Chắc chắn, rất khó để tìm ra thông điệp từ cấu trúc của nó và phải mất một số phỏng đoán có giáo dục, nhưng bạn cần lưu ý rằng máy tính làm việc này tốt hơn chúng ta rất nhiều. Điều này có nghĩa là chúng có thể được sử dụng để tìm ra các mã phức tạp hơn nhiều trong thời gian ngắn hơn nhiều, dựa trên những manh mối xuất phát từ cấu trúc và các yếu tố khác.

Nếu cấu trúc có thể dẫn đến một mã bị bẻ khóa và tiết lộ nội dung của tin nhắn, thì chúng ta cần một số cách để ẩn cấu trúc để giữ an toàn cho tin nhắn. Điều này đưa chúng ta đến đệm.

Khi một tin nhắn được đệm, dữ liệu ngẫu nhiên được thêm vào để ẩn các đầu mối định dạng ban đầu có thể dẫn đến một tin nhắn được mã hóa bị phá vỡ. Với RSA, mọi thứ phức tạp hơn một chút, bởi vì khóa được mã hóa không có định dạng rõ ràng của một chữ cái giúp cung cấp cho chúng tôi manh mối trong ví dụ trên của chúng tôi.

Mặc dù vậy, đối thủ có thể sử dụng một số cuộc tấn công để khai thác các thuộc tính toán học của mã và phá vỡ dữ liệu được mã hóa. Do mối đe dọa này, việc triển khai RSA sử dụng các lược đồ đệm như OAEP để nhúng dữ liệu bổ sung vào tin nhắn. Thêm phần đệm này trước khi tin nhắn được mã hóa giúp RSA an toàn hơn nhiều.

Ký tin nhắn

RSA có thể được sử dụng cho nhiều hơn là chỉ mã hóa dữ liệu. Các thuộc tính của nó cũng làm cho nó trở thành một hệ thống hữu ích cho xác nhận rằng một tin nhắn đã được gửi bởi thực thể người đã tuyên bố đã gửi nó, cũng như chứng minh rằng một tin nhắn đã bị thay đổi hoặc giả mạo.

Khi ai đó muốn chứng minh tính xác thực của tin nhắn của họ, họ có thể tính toán một băm (một hàm lấy dữ liệu có kích thước tùy ý và biến nó thành giá trị có độ dài cố định) của bản rõ, sau đó ký tên bằng khóa riêng của chúng. Họ ký băm bằng cách áp dụng cùng một công thức được sử dụng trong giải mã (m = cd mod n). Khi tin nhắn đã được ký, họ gửi chữ ký số này cho người nhận cùng với tin nhắn.

Nếu người nhận nhận được tin nhắn có chữ ký điện tử, họ có thể sử dụng chữ ký để kiểm tra xem tin nhắn có được ký xác thực bằng khóa riêng của người tuyên bố đã gửi nó không. Họ cũng có thể xem liệu tin nhắn đã bị thay đổi bởi những kẻ tấn công sau khi nó được gửi đi.

Để kiểm tra chữ ký số, trước tiên người nhận sử dụng cùng hàm băm để tìm giá trị băm của tin nhắn họ nhận được. Người nhận sau đó áp dụng người gửi khóa công khai chữ ký số, sử dụng công thức mã hóa (c = me mod n), để cung cấp cho họ hàm băm của chữ ký số.

Bởi so sánh hàm băm của tin nhắn đã nhận được cùng với hàm băm từ chữ ký số được mã hóa, người nhận có thể cho biết tin nhắn có xác thực không. Nếu hai giá trị giống nhau, thông báo sẽ không bị thay đổi kể từ khi được ký bởi người gửi ban đầu. Nếu thông điệp đã bị thay đổi bởi ngay cả một ký tự, giá trị băm sẽ hoàn toàn khác.

Bảo mật RSA & các cuộc tấn công

Giống như hầu hết các hệ thống mật mã, tính bảo mật của RSA phụ thuộc vào cách nó được triển khai và sử dụng. Một yếu tố quan trọng là kích thước của chìa khóa. Các số lượng bit trong một khóa càng lớn (về cơ bản là khóa đó dài bao nhiêu), càng khó phá vỡ các cuộc tấn công chẳng hạn như vũ phu và bao thanh toán.

Do các thuật toán khóa bất đối xứng như RSA có thể bị phá vỡ bởi hệ số nguyên, trong khi các thuật toán khóa đối xứng như AES không thể, các khóa RSA cần phải dài hơn nhiều để đạt được mức bảo mật tương tự.

Hiện tại, kích thước khóa lớn nhất đã được bao gồm là 768 bit. Điều này đã được thực hiện bởi một nhóm các học giả trong khoảng thời gian hai năm, sử dụng hàng trăm máy móc.

Kể từ khi bao thanh toán được hoàn thành vào cuối năm 2009 và sức mạnh tính toán đã tăng lên đáng kể kể từ thời điểm đó, có thể giả định rằng một nỗ lực có cường độ tương tự bây giờ có thể tạo ra khóa RSA lớn hơn nhiều.

Mặc dù vậy, thời gian và tài nguyên cần thiết cho loại tấn công này đưa nó ra khỏi tầm với của hầu hết các tin tặc và đi vào vương quốc của các quốc gia. Độ dài khóa tốt nhất để sử dụng sẽ phụ thuộc vào mô hình mối đe dọa cá nhân của bạn. Viện tiêu chuẩn và công nghệ quốc gia đề xuất kích thước khóa tối thiểu là 2048-bit, nhưng các phím 4096 bit cũng được sử dụng trong một số tình huống mức độ đe dọa cao hơn.

Bao thanh toán chỉ là một cách mà RSA có thể bị phá vỡ. Một số cuộc tấn công khác có khả năng phá vỡ mã hóa với số lượng tài nguyên nhỏ hơn, nhưng chúng phụ thuộc vào việc triển khai và các yếu tố khác, không nhất thiết phải là chính RSA. Một số trong số này bao gồm:

Các số nguyên tố có thực sự ngẫu nhiên không?

Một số triển khai RSA sử dụng các trình tạo số ngẫu nhiên yếu để đưa ra các số nguyên tố. Nếu những con số này không đủ ngẫu nhiên, điều đó giúp những kẻ tấn công dễ dàng hơn trong việc tạo ra chúng và phá vỡ mã hóa. Vấn đề này có thể tránh được bằng cách sử dụng trình tạo số giả ngẫu nhiên an toàn bằng mật mã.

Tạo khóa kém

Các khóa RSA cần nằm trong một số tham số nhất định để chúng được an toàn. Nếu số nguyên tố p và q quá gần nhau, chìa khóa có thể dễ dàng được phát hiện. Tương tự như vậy, số d mà chiếm một phần của khóa riêng không thể quá nhỏ. Một giá trị thấp làm cho nó dễ dàng để giải quyết. Điều quan trọng là những con số này có độ dài phù hợp để giữ chìa khóa của bạn an toàn.

Tấn công kênh bên

Đây là một kiểu tấn công không thể phá vỡ RSA trực tiếp, nhưng thay vào đó sử dụng thông tin từ việc triển khai để cung cấp cho kẻ tấn công gợi ý về quá trình mã hóa. Những cuộc tấn công này có thể bao gồm những thứ như phân tích lượng điện năng đang được sử dụng, hoặc là phân tích dự đoán chi nhánh, trong đó sử dụng các phép đo thời gian thực hiện để khám phá khóa riêng.

Một kiểu tấn công kênh bên khác được gọi là tấn công thời gian. Nếu kẻ tấn công có khả năng đo thời gian giải mã trên máy tính mục tiêu của họ đối với một số tin nhắn được mã hóa khác nhau, thông tin này có thể giúp kẻ tấn công xác định khóa riêng của mục tiêu.

Hầu hết các triển khai RSA đều tránh được cuộc tấn công này bằng cách thêm giá trị một lần trong quá trình mã hóa, loại bỏ mối tương quan này. Quá trình này được gọi là chói mắt mật mã.

Mã hóa RSA có an toàn cho tương lai không?

Tin tốt là RSA được coi là an toàn để sử dụng, bất chấp những cuộc tấn công có thể xảy ra. Hãy cẩn thận là nó cần được thực hiện chính xác và sử dụng một khóa nằm trong các tham số chính xác. Như chúng ta vừa thảo luận, việc triển khai don don sử dụng phần đệm, sử dụng các số nguyên tố có kích thước không phù hợp hoặc có các lỗ hổng khác không thể được coi là an toàn.

Nếu bạn muốn sử dụng mã hóa RSA, đảm bảo rằng bạn đang sử dụng khóa ít nhất 1024 bit. Những người có mô hình mối đe dọa cao hơn nên bám vào các khóa 2048 hoặc 4096 bit nếu họ muốn sử dụng RSA một cách tự tin. Miễn là bạn nhận thức được những điểm yếu mà RSA có và sử dụng nó một cách chính xác, bạn nên cảm thấy an toàn khi sử dụng RSA để chia sẻ khóa và các tác vụ tương tự khác yêu cầu mã hóa khóa chung.

Xem thêm: Các loại mã hóa phổ biến được giải thích