Chữ ký số là gì và chúng hoạt động như thế nào?

Chữ ký điện tử giống như các phiên bản điện tử của chữ ký viết tay của bạn. Họ cho phép mọi người kiểm tra tính xác thực và tính toàn vẹn của dữ liệu, cũng như ngăn chặn người ký không thể từ chối (từ chối) sự tham gia của họ.

Các đặc tính này đã dẫn đến việc áp dụng chữ ký số trong một loạt các ứng dụng, bao gồm nhiều giao thức bảo mật, email bảo mật và trong quản lý quyền kỹ thuật số.

Trong bài viết này, chúng tôi sẽ thảo luận chữ ký số là gì, nơi chúng được sử dụng, cũng như các chi tiết kỹ thuật của hai trong số các thuật toán phổ biến nhất, RSA và DSA.

Chữ ký số là gì?

Như đã nêu ở trên, chữ ký số cung cấp cho chúng ta ba thuộc tính rất quan trọng. Đây là xác thực, tính toàn vẹn và không thoái thác.

Xác thực là quá trình xác minh rằng cá nhân gửi tin nhắn thực sự là người họ nói chứ không phải là kẻ mạo danh.

Các chính trực dữ liệu hoặc tin nhắn đề cập đến việc liệu nó đã đến trạng thái như khi nó được gửi chưa. Nếu một tin nhắn đã bị thay đổi hoặc giả mạo, nó sẽ không còn giữ được tính toàn vẹn của nó.

Nếu dữ liệu hoặc tin nhắn là không thoái thác, điều đó có nghĩa là tác giả của nó không thể tranh cãi rằng họ là người tạo ra tài liệu thực sự. Khách sạn này lấy đi sự từ chối hợp lý, hoặc cũ Xin lỗi, bạn tôi đang sử dụng tài khoản của tôi..

Miễn là khóa riêng của cá nhân chưa bị xâm phạm, chữ ký số có thể cung cấp cả ba thuộc tính này cho dữ liệu.

Bạn có thể tự hỏi tại sao chúng ta cần những tài sản này ở nơi đầu tiên. Hãy để Lùi lùi lại một bước và suy nghĩ về cách chúng ta làm mọi thứ trong cuộc gặp mặt trực tiếp.

Hãy nói rằng bạn nợ bạn của mình Mike 100 đô la. Bạn là một người tốt, vì vậy bạn rất vui khi trả lại cho anh ấy khi bạn nhận được tiền.

Cách tốt nhất để làm điều đó là chỉ cần đưa hóa đơn 100 đô la cho Mike. Bạn đã biết anh ta trong nhiều năm và biết anh ta trông như thế nào, vì vậy nó sẽ là dễ dàng xác minh danh tính của anh ấy và do đó xác thực rằng bạn đang đưa tiền cho đúng người.

Nếu bạn thực sự là hậu môn, bạn thậm chí có thể kiểm tra ID của anh ấy và yêu cầu anh ấy ký biên nhận viết tay cho bạn. Chữ ký trên biên lai sẽ cung cấp cho nó tính toàn vẹn và làm cho nó không bị từ chối.

Điều gì sẽ xảy ra nếu thay vì thực hiện giao dịch trực tiếp, bạn nhận được một cuộc gọi từ ai đó nói rằng họ là Mike và bạn nên gửi 100 đô la đến số tài khoản 12345678.

Tuy nhiên, bạn không có âm thanh như Mike, bạn nói.

“Tôi bị cảm lạnh. Gửi ngay bây giờ, tôi cần tiền.

Bạn sẽ gửi tiền chứ? Chắc là không.

Không có cách nào để biết liệu đó thực sự là Mike hay số tài khoản chính xác. Đối với tất cả những gì bạn biết, nó có thể là một kẻ mạo danh đang cố gắng đánh cắp từ bạn. Thay vì chuyển tiền ngay lập tức, tốt nhất là đợi cho đến khi bạn gặp Mike để bạn có thể trực tiếp đưa tiền cho anh ấy.

Giống như trong kịch bản trên, chúng ta thường xuyên gặp phải những tình huống cần phải xác minh danh tính của một bên hoặc tính toàn vẹn của dữ liệu trong thế giới trực tuyến. Đó là lý do tại sao chữ ký số đã tăng lên như một cơ chế có thể cung cấp các tài sản này và tạo điều kiện cho các giao dịch trực tuyến an toàn.

Không có họ, chúng tôi có thể không biết mình đang nói chuyện với ai, không thể chắc chắn liệu dữ liệu có bị giả mạo hay không và người đó có thể phủ nhận rằng họ có trách nhiệm.

Việc sử dụng chữ ký số

Các tính chất của chữ ký số làm cho chúng hữu ích trong nhiều ứng dụng. Chúng thường được sử dụng bởi chính chúng hoặc kết hợp với mã hóa trong một loạt các giao thức bảo mật khác nhau, chẳng hạn như:

• IPsec
• SSH
• TLS

Chúng cũng thường xuyên được sử dụng trong Quản lý bản quyền kỹ thuật số, trong công nghệ chuỗi khối, trong Quản lí hợp đồng các ứng dụng, như là một phần của Phân phối phần mềm, và trong tài chính.

Lịch sử chữ ký số

Ý tưởng về chữ ký số lần đầu tiên được đưa ra bởi các nhà mật mã học nổi tiếng Whitfield Diffie và Martin Hellman trong bài báo năm 1976 của họ Hướng đi mới trong Mật mã học. Năm 1978, Ronald Rivest, Adi Shamir và Len Adeld đã đưa thuật toán RSA vào chế độ công khai, có thể được sử dụng để tạo chữ ký số không an toàn.

Phải mất một thập kỷ nữa để chữ ký số xuất hiện trong một ứng dụng rộng rãi: phát hành IBM Lotus Lotus Notes 1.0. Từ đó trở đi, chữ ký số bắt đầu được áp dụng rộng rãi hơn khi các kỹ thuật mới xuất hiện và nhu cầu kiểm tra tính xác thực và kiểm tra tính toàn vẹn trực tuyến tăng lên.

Giới thiệu ngắn gọn về mật mã khóa công khai

Trước khi chúng tôi nhảy vào chữ ký số, điều tốt nhất là bao quát một số khía cạnh quan trọng của mật mã khóa công khai, hình thành nên cơ sở của cách chữ ký số hoạt động.

Nếu bạn tương đối mới với mật mã, hệ thống mà bạn sẽ quen thuộc nhất là mã hóa khóa đối xứng. Điều này chỉ có nghĩa là cùng một khóa (tương tự như mật khẩu, nhưng có một số khác biệt) được sử dụng để cả mã hóa và giải mã dữ liệu.

Mã hóa khóa công khai là một cuộc cách mạng, vì nó liên quan sử dụng các khóa riêng cho quá trình mã hóa và giải mã, dẫn đến một loạt các ứng dụng mật mã khác nhau. Hai khóa này tạo thành một cặp khóa, bao gồm khóa chung và khóa riêng. Khóa công khai rõ ràng có thể được chia sẻ công khai, trong khi khóa riêng phải được giữ bí mật để hệ thống được an toàn.

Hai cách sử dụng phổ biến nhất của mật mã khóa công khai là mã hóa và chữ ký số.

Mã hóa

Một trong những tính năng đột phá của mật mã khóa công khai là nó cho phép các bên chưa bao giờ gặp nhau tự tin gửi tin nhắn cho nhau. Người gửi tìm kiếm khóa chung của người nhận mong muốn của họ (có thể tìm thấy khóa này trên các máy chủ khóa công khai, trên trang web cá nhân hoặc đơn giản bằng cách hỏi từng cá nhân), sau đó mã hóa tin nhắn bằng khóa này, trước khi gửi cho người nhận.

Người nhận là người duy nhất có thể truy cập tin nhắn mà Giả sử rằng khóa riêng chưa bị xâm phạm bằng cách giải mã nó bằng khóa riêng của họ. Mặc dù khóa chung được sử dụng để mã hóa tin nhắn, nhưng nó chỉ có thể được giải mã bằng khóa riêng. Nếu người nhận muốn trả lời, họ tìm thấy khóa chung của người gửi ban đầu, sau đó lặp lại quy trình.

Xem thêm: Các loại mã hóa phổ biến được giải thích

Chữ ký số hoạt động như thế nào?

Như chúng tôi đã nói, chữ ký điện tử được sử dụng để xác thực, để xem liệu dữ liệu có bị giả mạo hay không và để cung cấp không thoái thác. Có một loạt các cơ chế khác nhau có thể được sử dụng cho chữ ký điện tử và mỗi cơ chế có một số thay đổi nhỏ trong cách chúng được cấu trúc.

Nói chung, các thuật toán này cần phải bao gồm ba thuật toán phụ:

• Một thuật toán tạo khóa – Thuật toán này tạo ra một cặp khóa ngẫu nhiên cho người dùng. Các số liên quan đến cặp khóa cần tuân theo một số tham số nhất định để được coi là an toàn. Hai trong số các khía cạnh quan trọng nhất là các con số đủ ngẫu nhiên và có kích thước phù hợp.
• Một thuật toán để ký dữ liệu – Khi người dùng có khóa của họ, có những cách cụ thể để áp dụng chúng vào dữ liệu trong quy trình chữ ký.
• Một thuật toán để xác minh chữ ký – Tương tự như vậy, xác minh chữ ký tuân theo quy trình được xác định trước.

Để một hệ thống chữ ký số có hiệu quả, nó cần được cấu trúc theo cách:

• Dữ liệu được ký bằng khóa riêng là được xác minh với cùng khóa công khai phù hợp với cá nhân.
• Về cơ bản là không thể (sử dụng công nghệ và kỹ thuật hiện tại) để giả mạo chữ ký hợp lệ mà không cần biết khóa riêng của riêng lẻ.

Một số chương trình chữ ký số phổ biến nhất bao gồm RSA, DSA, EcDSA và EdDSA.

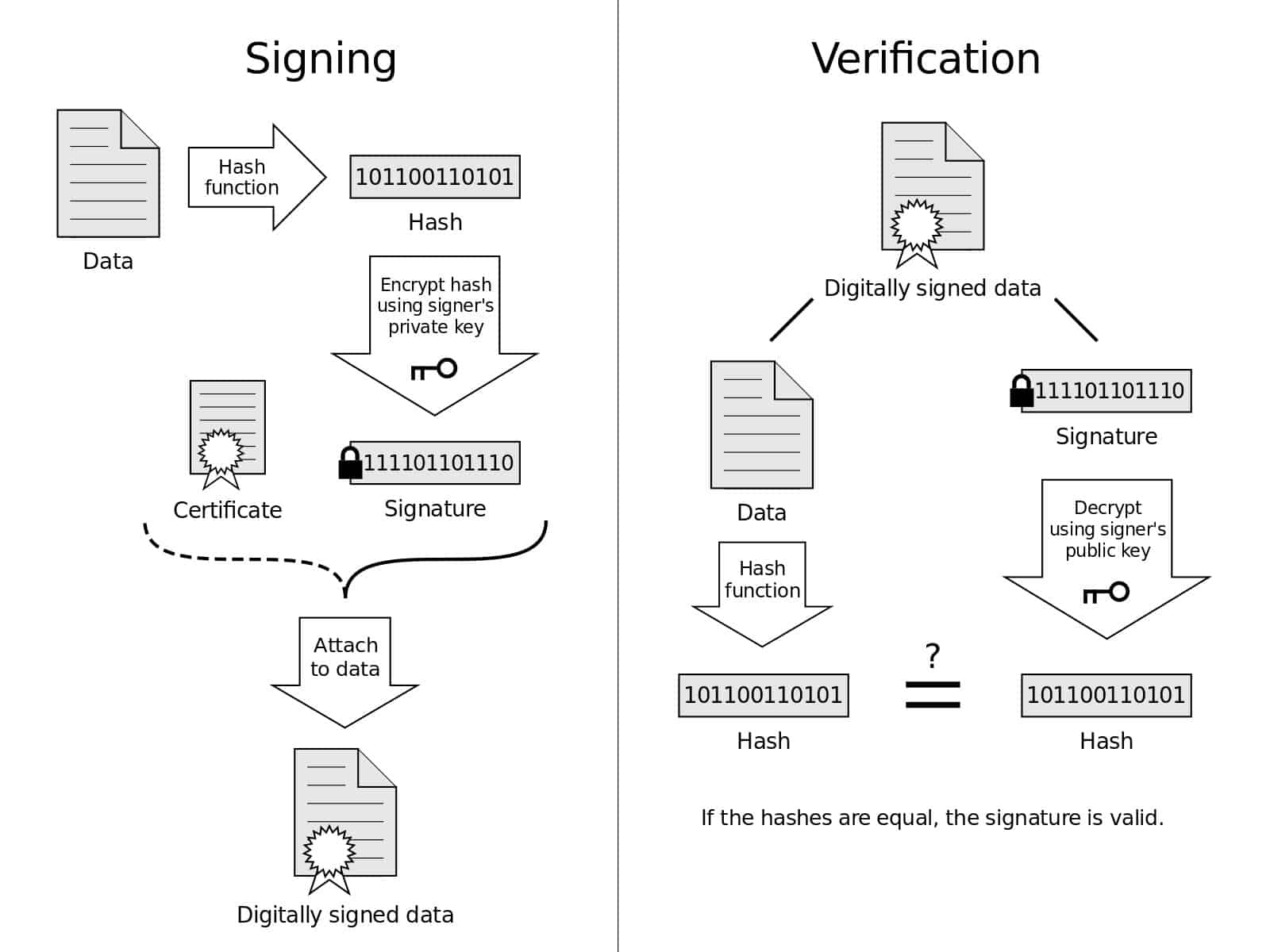
Hình ảnh này thể hiện trực quan các quy trình ký và xác minh. Sơ đồ chữ ký số bởi Acdx được cấp phép theo Muff

RSA

RSA là thuật toán chữ ký số đầu tiên, nhưng nó cũng có thể được sử dụng để mã hóa khóa công khai. Trong bài viết này, chúng tôi sẽ bỏ qua khía cạnh mã hóa, nhưng bạn có thể tìm hiểu thêm về nó trong bài viết toàn diện của chúng tôi bao gồm RSA là gì và cách thức hoạt động của nó.

Tạo khóa RSA

Trong triển khai RSA an toàn, các cặp khóa thường sẽ được thiết lập tự động theo quy trình sau:

Thế hệ chính

Hai số nguyên tố riêng lẻ được chọn, p và q. Kích thước chính xác của các số nguyên tố này sẽ thay đổi tùy thuộc vào kích thước khóa. Ngày nay, thường sử dụng tối thiểu các khóa RSA 2048 bit để bảo mật đầy đủ, vì vậy chúng tôi đang nói về hai số nguyên tố nhân để tạo ra số 2048 bit.

2048 bit là một kích thước trong hệ thống số nhị phân. Nếu một số kích thước này được chuyển đổi sang hệ thập phân quen thuộc hơn của chúng tôi, thì nó sẽ dài khoảng:

790279459827301874397592846209502937592870495029380589710393

70190192098393759701938508910395107305841536875762873659842599

382485698437658276348791283758273659287368427368472893857575872

4958729873958729835792875982795837529876348273685729843579348

7958458720948602984912837502948019371092482793857928739548772

3975928375924785938670353103799581093750193850791345986792384

7378267352673547623568734869386945673456827659493849024875809

6039429837592834759348759384759284780634701938091803984091804

9810938592873995710901985013984019835091835019830910791803958

10395190395180935310938538584843530193840198340918093851098383

09180019

Các số nguyên tố trong RSA phải được chọn ngẫu nhiên và phải có độ dài tương tự.

Trong ví dụ của chúng tôi, chúng tôi sẽ sử dụng các số nhỏ hơn nhiều để làm cho mọi thứ dễ hiểu hơn. Xin lưu ý rằng việc sử dụng các khóa có kích thước này sẽ làm cho chữ ký số trở nên tầm thường thành giả. Đây là lý do tại sao các giá trị lớn như vậy được sử dụng trong thực tế.

Hãy nói rằng:

p = 13

q = 17

Bước đầu tiên sẽ là tính toán mô đun n sử dụng công thức sau:

n = pq

n = 13 x 17

n = 221

Giá trị của n cũng là độ dài khóa.

Hàm toàn phần của Carmichael

Bây giờ chúng ta có giá trị cho n, Bước tiếp theo là sử dụng chức năng toàn bộ của Carmichael từ:

λ(n) = = lcm (p – 1, q – 1)

Có một vài điều mà bạn cần hiểu:

• λ(n) có nghĩa là toàn bộ giá trị của Carmichael n
• lcm đại diện cho hệ số nhân chung thấp nhất. Đây là con số chung thấp nhất mà cả hai p-1 và q-1 có thể chia thành

Hãy để cắm các số liệu của chúng tôi vào phương trình:

λ(221) = lcm (13 – 1, 17 – 1)

λ(221) = lcm (12, 16)

Nếu bạn giỏi toán tinh thần, bạn có thể đã tìm ra rằng 48 là hệ số chung thấp nhất của cả hai 12 và 16. Điều này là do 48 là số nhỏ nhất mà cả hai số này có thể phù hợp với (12 x 4 = 48, 16 x 3 = 48). Vì thế:

λ(221) = 48

Sắp có khóa công khai

Trong RSA, khóa chung bao gồm giá trị n (mà chúng tôi đã tính như 221) và e. Vì khóa chung được chia sẻ tự do, giá trị cho e không phải là một bí mật. Trên thực tế, nó thường đặt ở mức 65.537 trong thực tế, vì số lượng lớn hơn sẽ làm chậm quá trình mã hóa. Trong ví dụ của chúng tôi, chúng tôi sẽ thiết lập e đến 5, chỉ để làm cho nó một số nhỏ và đơn giản để làm việc với.

Do đó, khóa chung cho ví dụ này bao gồm 221 và 5. Chúng tôi sẽ đề cập chi tiết cụ thể về cách áp dụng khóa chung trong các phần sau.

Tìm ra khóa riêng

Giống như khóa công khai của chúng tôi được tạo thành từ hai số, khóa riêng của chúng tôi cũng vậy. Khóa riêng bao gồm d và e. Chúng tôi đã biết giá trị cho e (5), và chúng ta có thể sử dụng công thức sau để tìm d:

d = 1 /e mod λ(n)

Lưu ý rằng mod chỉ tượng trưng cho một hoạt động modulo, điều này thường có nghĩa là bạn phải tìm phần còn lại một khi bạn chia bên trái cho bên phải. Ví dụ:

17 mod 3 = 2

Điều này là do 3 phù hợp với 17 tổng cộng 5 lần, với 2 phần còn lại.

Ví dụ của chúng tôi là một chút khác nhau. Các “1 /e modPhân đoạn của phương trình có thể xuất hiện để bảo bạn chia 1 bởi e, nhưng nó thực sự là không. Nó khó hiểu, nhưng đây là một cách để thể hiện mô đun nghịch đảo. Phương trình thực sự bảo chúng ta tính toán nghịch đảo mô đun của e và λ(n).

Nghịch đảo mô-đun thường được dẫn xuất bằng thuật toán Euclide mở rộng, nhưng chúng tôi đã thắng được trong bài viết này. Thay vào đó, chúng tôi sẽ chỉ sử dụng một máy tính trực tuyến để làm cho mọi thứ dễ dàng hơn.

Bây giờ, chúng tôi đã nhận được điều đó, hãy để nhập các giá trị của chúng tôi vào công thức:

d = 1/5 mod 48

Để tìm d, tất cả những gì chúng ta phải làm là nhập giá trị của chúng tôi cho e (5) vào máy tính trực tuyến nơi nó nói số nguyên, sau đó giá trị của chúng tôi cho λ(n), đó là 48, nó nói ở đâu modulo.

Điều này cho chúng ta một kết quả của 29 theo máy tính trực tuyến. Do đó, khóa riêng của chúng tôi sẽ được tạo thành:

e = = 5

d = = 29.

Bây giờ chúng tôi đã tạo cả hai khóa của mình, câu hỏi tiếp theo là, chúng tôi làm gì với chúng? Chà, chúng ta có thể sử dụng chúng để mã hóa và giải mã tin nhắn thông qua mật mã khóa công khai, nhưng bài viết này là về chữ ký số, vì vậy chúng tôi sẽ tập trung vào đó.

Ký dữ liệu số với RSA

Hãy nói với ai đó rằng ai đó muốn gửi tin nhắn cho bạn của họ, nhưng họ muốn đảm bảo rằng người bạn đó có thể xác minh tính xác thực và tính toàn vẹn của tin nhắn. Họ có thể làm điều này bằng cách sử dụng chữ ký số RSA để ký tin nhắn.

Bước đầu tiên là chạy toàn bộ tin nhắn thông qua hàm băm. Đây là các hàm một chiều luôn cung cấp cùng một đầu ra cho một đầu vào nhất định. Các hàm băm an toàn về cơ bản là không thể đảo ngược, điều đó có nghĩa là đầu ra không thể được sử dụng để tìm ra đầu vào. Cũng không khả thi khi hai tin nhắn riêng biệt có cùng một đầu ra.

Bạn có thể tìm hiểu thêm về các hàm băm trong Băm là gì? Phần của bài viết của chúng tôi, Mã hóa, băm, muối – những gì khác biệt?

Hãy nói rằng chúng tôi muốn ký điện tử vào tin nhắnHôm nay trời nóngĐể người nhận của chúng tôi có thể biết liệu tin nhắn có xác thực hay không và liệu nó có bị giả mạo hay không. Vì vậy, chúng tôi sẽ điều hànhHôm nay trời nóngThông qua một hàm băm.

Hiểu hàm băm

Ngày nay, hàm băm an toàn được sử dụng phổ biến nhất là SHA-256. Khi chúng tôi gửi thông điệp của mình thông qua máy tính SHA-256 trực tuyến, nó sẽ cho chúng tôi một kết quả như sau:

efbcf22b4cd04d49daa87cfbda7d2313cc665c35bc9e18954af16c104a731952

Điều này đặt ra một vài vấn đề cho ví dụ của chúng tôi. Đầu tiên là nó không phải là số thập phân giống như số mà hầu hết mọi người thường sử dụng. Bạn có thể nhận thấy rằng có những chữ cái trong số này và chúng chỉ đi lên f. Điều này cho chúng ta một manh mối rằng nó thực sự là một số thập lục phân.

Các hệ thập lục phân dựa trên cơ sở 16, thay vì cơ sở 10, Giống như hệ thống số mà chúng ta thường sử dụng. Điều này có nghĩa là, thay vì đếm theo bội số của 10, nó tính theo bội số của 16 và 6 chữ cái đầu tiên trong bảng chữ cái của chúng tôi được sử dụng để tạo thành các số phụ này. Một số như thế này có thể được chuyển đổi thành hệ thống thập phân hàng ngày của chúng tôi, nhưng điều đó ra khỏi phạm vi của bài viết này.

Vấn đề thứ hai mà chúng tôi có là đây là một con số thực sự lớn. Nếu nó được chuyển đổi thành số thập phân, nó sẽ còn dài hơn nữa. Vì chúng tôi đang hướng đến sự đơn giản trong hướng dẫn này, nên việc chạy các phép tính với số lượng lớn như vậy sẽ khiến mọi thứ trở nên quá khó hiểu để có được các khái niệm cơ bản xuyên suốt.

Với ý tưởng thể hiện cách thức chữ ký số RSA hoạt động theo cách dễ hiểu, chúng tôi đã thắng được khi sử dụng giá trị băm lớn như vậy trong ví dụ sau. Thay vào đó, chúng tôi sẽ giả vờ rằng giá trị băm của hungHôm nay trời nóng” chỉ đơn giản là 10.

Chúng ta cũng sẽ phải giả vờ, giống như bất kỳ hàm băm thực sự nào, bất cứ khi nào chúng ta đặt đầu vào của trò chơi It It nóng ngày hôm nay qua chức năng băm, nó sẽ luôn trả về giá trị của 10. Để phù hợp với cách các hàm băm thường hoạt động, chúng ta sẽ phải giả vờ rằng nó rất khó có thể cho bất kỳ đầu vào nào khác có cùng giá trị. Tương tự như vậy, chúng ta cần phải giả vờ rằng nó cũng không khả thi để tìm ra đầu vào ban đầu của chúng tôi từ giá trị này. Những đặc tính này là những gì làm cho băm vô cùng hữu ích.

Cách khóa riêng của người gửi được sử dụng để ký điện tử giá trị băm

Người gửi của chúng tôi đã gõ tin nhắn của họ, sau đó đặt nó thông qua hàm băm mà chúng tôi đang giả vờ trả về giá trị là 10. Khi người gửi có hàm băm của tin nhắn, họ có thể tạo chữ ký số bằng cách áp dụng khóa riêng của họ cho giá trị băm theo công thức sau:

m (c) = = cd mod n

Đây thực sự là công thức để giải mã dữ liệu đã được mã hóa bằng khóa công khai của người nhận, nhưng nó cũng được sử dụng để ký các tài liệu kỹ thuật số.

Khi nói đến chữ ký số:

• Giá trị của m (c) sẽ là chữ ký.
• Giá trị của c là hàm băm của tin nhắn (10).
• Giá trị của d là một phần của khóa riêng của người gửi, mà chúng tôi đã nhận được trước đó (29).
• Các mod chức năng là hoạt động còn lại mà chúng tôi đã đề cập trước đó.
• Giá trị của n là một phần khác của khóa riêng của người gửi, mà chúng tôi đã tính khi bắt đầu (221).

Vì vậy, hãy để Lít đưa tất cả vào công thức của chúng tôi:

m (c) = 1029 mod 221

    m (c) = 100.000.000.000.000.000.000.000.000 mod mod 221

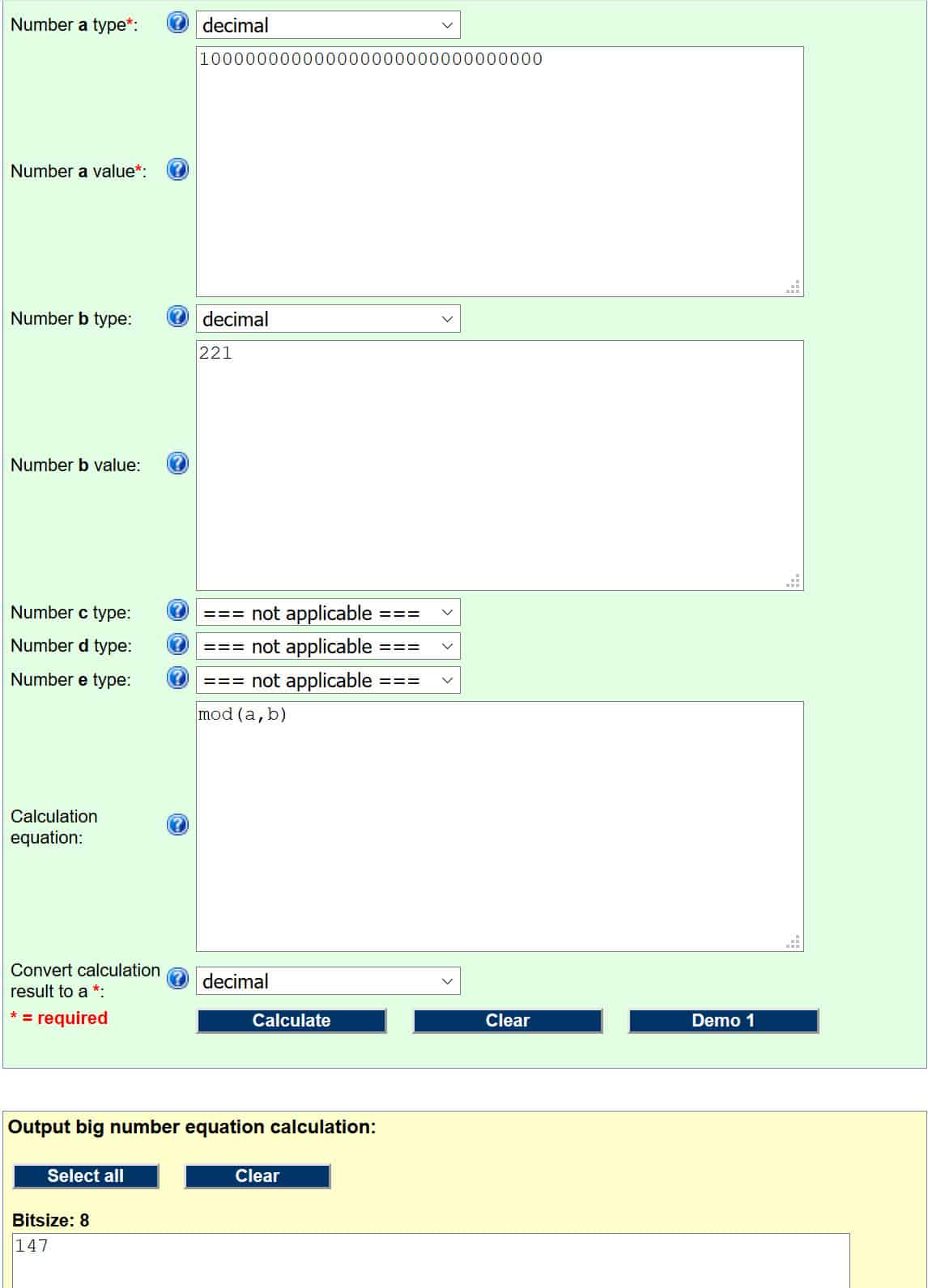
Hãy để Lừa chạy nó thông qua máy tính modulo sau (chúng tôi đã giải thích cách các hoạt động này hoạt động theo Tìm ra khóa công khai phần). Để nó hoạt động chính xác, chúng ta cần đặt đầu vào là:

• Con số một kiểu – số thập phân
• Con số một giá trị – 100000000000000000000000000000
• Con số b kiểu – số thập phân
• Con số b giá trị – 221
• Phương trình tính toán (đây chỉ là mã cho máy tính biết thao tác nào sẽ thực hiện. Mã này và các mã khác có thể được tìm thấy trên trang web được liên kết phía trên phần đầu vào) – mod (a, b)

Nếu bạn đã làm mọi thứ đúng cách, nó sẽ trông như thế này:

Số trong hộp màu vàng là câu trả lời của chúng tôi, vì vậy chữ ký số cho hàm băm của tin nhắn là 147.

Để chứng minh tính xác thực và tính toàn vẹn của tin nhắn, cùng với việc cung cấp không thoái thác, người gửi của chúng tôi sẽ truyền tin nhắnHôm nay trời nóngBên cạnh chữ ký số của 147 để người nhận mong muốn của họ. Chỉ cần nhớ rằng chúng tôi đã sử dụng một giá trị nhỏ cho hàm băm để đơn giản hóa mọi thứ, thay vì hàm băm thực sự của tin nhắn.

Xác minh chữ ký số

Chữ ký số chỉ hữu ích nếu chúng tôi có thể xác minh xem chúng có hợp pháp không. Miễn là khóa riêng của người gửi không bị xâm phạm, người nhận có thể kiểm tra xem tin nhắn có xác thực hay không và giữ lại tính toàn vẹn của nó bằng cách áp dụng công thức sau cho chữ ký số:

    c (m) = = me mod n

Ngược lại quá trình ký, đây thực sự là công thức được sử dụng để mã hóa dữ liệu trong RSA. Khi chúng tôi sử dụng công thức này để xác minh chữ ký:

• Giá trị của c (m) sẽ là giá trị băm của người gửi tại thời điểm họ ký (do cấu trúc của thuật toán khóa công khai RSA, áp dụng khóa chung của người gửi thông qua công thức này sẽ hoàn tác thao tác ký mà chúng ta vừa thực hiện, để lại cho chúng ta hàm băm giả ban đầu ).
• Giá trị của m là chữ ký số (147).
• Giá trị của e là một phần của khóa công khai người gửi, mà chúng tôi đã nhận được trước đó (5).
• Các mod chức năng là hoạt động còn lại mà chúng tôi đã đề cập trước đó.
• Giá trị của n là một phần khác của khóa công khai người gửi, mà chúng tôi đã tính khi bắt đầu (221).

Hãy để Lừa ném tất cả vào công thức:

    c (m) = 1475 mod 221

    c (m) = 68.641.485.507 mod 221

Hãy để sử dụng máy tính modulo giống như trước đây và giữ mọi thứ giống nhau, ngoại trừ:

• Con số một giá trị – 68.641.485.507

Nếu bạn đã nhập chính xác, bạn sẽ nhận được kết quả:

c (m) = 10

Bây giờ người nhận đã tính giá trị băm từ chữ ký số, bước tiếp theo của họ là tính giá trị băm của tin nhắn mà họ nhận được, HồiHôm nay trời nóngMùi. Nếu bạn còn nhớ trước đó, chúng tôi đã thực sự sử dụng hàm băm SHA-256 thực sự của tin nhắn, vì số lượng quá lớn và làm cho ví dụ trở nên quá phức tạp.

Thay vào đó, chúng tôi đã giả vờ rằng hàm băm thực sự mang lại cho chúng tôi số lượng nhỏ, 10, cho đầu vào của chúng tôi. Vì các hàm băm luôn xuất kết quả giống nhau cho một đầu vào nhất định, khi người nhận của chúng tôi đặtHôm nay trời nóngThông qua chức năng băm tưởng tượng của chúng tôi, họ cũng đã nhận được giá trị của 10.

Quá trình xác minh chữ ký dẫn đến hai giá trị. Giá trị đầu tiên là hàm băm như khi người gửi ký điện tử với khóa riêng của họ. Chúng tôi đã tính toán điều này ở trên bằng cách sử dụng khóa công khai của người gửi.

Giá trị thứ hai là hàm băm của tin nhắn mà người nhận nhận được. Điều này được tính bằng cách sử dụng cùng hàm băm mà người gửi đã sử dụng để băm thông điệp ban đầu của họ. Hai giá trị này sau đó được so sánh và nếu các giá trị là như nhau, thì chúng ta có thể giả sử rằng thông điệp là xác thực, giữ nguyên tính toàn vẹn của nó và rằng nó không bị từ chối. Tất nhiên, điều này giả định rằng khóa riêng của người gửi không bị xâm phạm.

Vì ví dụ của chúng tôi trả về giá trị là 10 cho hàm băm khi được người gửi ký, cũng như giá trị của 10 là hàm băm của tin nhắn đã nhận được, chúng ta có thể giả sử rằng tin nhắn đóHôm nay trời nóng” đến từ người tuyên bố đã gửi nó và nó đã không bị thay đổi kể từ khi nó được gửi.

Nếu người nhận muốn trả lời để phóng viên của họ có thể xác minh tin nhắn của họ theo cùng một cách, toàn bộ quá trình được lặp lại, ngoại trừ khóa riêng tư và khóa công khai của người nhận được sử dụng cho quá trình ký và xác minh, tương ứng.

Tất cả các toán học này có thể đã đưa bạn ra khỏi toàn bộ ý tưởng về chữ ký số. Don Patrick lo lắng, vì việc triển khai RSA tự động hóa quá trình này, vì vậy bạn không nên giẫm đạp bất kỳ con số nào.

Ưu điểm của RSA & khuyết điểm

RSA là một trong những thuật toán chữ ký số được hỗ trợ và triển khai rộng rãi nhất, mặc dù có một động thái hướng tới các thuật toán mới hơn, hiệu quả hơn và an toàn hơn như ECDSA và EdDSA.

Khi so sánh với DSA (mà chúng tôi sẽ đề cập trong phần tiếp theo), RSA nhanh hơn trong việc xác minh chữ ký, nhưng chậm hơn trong việc tạo ra chúng. Vì chữ ký có xu hướng được tạo một lần và được xác minh nhiều lần, RSA thường được ưa thích hơn DSA.

DSA

Tính bảo mật của Thuật toán Chữ ký số dựa trên hai khái niệm toán học, bài toán logarit rời rạc và một số tính chất của lũy thừa mô đun. Đối với một số nhóm, không thể tính toán logarit rời rạc của họ với các kỹ thuật và công nghệ hiện tại.

Tạo khóa DSA

Để tạo khóa DSA, bước đầu tiên là chọn các tham số mà một nhóm người dùng trong cùng hệ thống có thể sử dụng để tạo cặp khóa.

Tạo các tham số

• Chọn một hàm băm – SHA-256 là tùy chọn phổ biến nhất để đáp ứng các yêu cầu bảo mật hiện đại.
• Giải quyết về độ dài khóa, L và N – Những ngày này, L phải dài ít nhất 2.048 bit, trong khi N nên có ít nhất 256 bit.
• Quyết định về một nguyên tố, q, đó là cùng chiều dài với N.
• Chọn một số nguyên tố, p, Ở đâu p-1 là bội số của q.
• Chọn một số, g, sử dụng công thức sau (trong đó h là một số tùy ý trong khoảng từ 1 đến p-1):

g = = h(p – 1) /q mod p

Thông thường, các giá trị này là số lượng rất lớn để làm cho thuật toán an toàn. Để giữ cho ví dụ của chúng tôi không quá khó để tính toán hoặc giải thích, chúng tôi sẽ sử dụng các số nhỏ hơn nhiều mà không thực sự an toàn. Hãy nói rằng:

    q = 5

    p = 11

Để tìm g, chúng tôi cắm số của chúng tôi vào công thức. Chúng tôi sẽ sử dụng 3 là giá trị của chúng tôi cho h:

g = 3 (11-1) / 5 mod 11

g = 32 mod 11

g = 9 mod 11

Chúng tôi sẽ sử dụng cùng một máy tính modulo như trong Cách khóa riêng của người gửi được sử dụng để ký điện tử giá trị băm phần. Các tham số sẽ giống nhau, ngoại trừ:

• Con số một giá trị – 9
• Con số b giá trị – 11

Nếu bạn đã nhập chính xác mọi thứ, nó sẽ cho bạn kết quả g của 9.

Tạo khóa người dùng

Người dùng cá nhân sau đó lấy các tham số này và sử dụng chúng để tạo thành cặp khóa của họ:

• Khóa riêng (x) là một số ở giữa 0 và q, mà chúng tôi đặt ở mức 5. Ví dụ của chúng tôi, chúng tôi sẽ chọn 2 là x, khóa riêng của chúng tôi.
• Khóa công khai (y) được tính bằng công thức sau:

    y = = gx mod p

Vì thế:

y = 92 mod 11

y = 81 mod 11

Chúng tôi sẽ sử dụng cùng một máy tính modulo một lần nữa. Các tham số sẽ giống nhau, ngoại trừ:

• Con số một giá trị – 81
• Con số b giá trị – 11

Nếu bạn đã nhập chính xác, bạn sẽ nhận được kết quả là y = 4. Do đó, khóa công khai là 4.

Bây giờ chúng tôi đã tạo ra tất cả các giá trị của chúng tôi, hãy để cho bạn một bản tóm tắt nhanh chóng. Các tham số cho hệ thống là:

• p = 11
• q = 5
• g = 9

Cặp chìa khóa của chúng tôi được tạo thành từ:

• Khóa riêng, x = 2
• Khóa công khai, y = 4

Ký dữ liệu số với DSA

Người gửi có thể sử dụng khóa riêng DSA của họ để ký dữ liệu kỹ thuật số, cho phép người nhận của họ xác minh xem tin nhắn có xác thực hay không và giữ nguyên tính toàn vẹn của nó. Nó cũng ngăn người gửi có thể từ chối tin nhắn.

Quá trình chữ ký bắt đầu bằng cách tạo ra một giá trị ngẫu nhiên k, đó là giữa 1 và q. Với ví dụ này, hãy để chỉ cần chọn 3 như số ngẫu nhiên của chúng tôi, k.

Sau đó chúng tôi làm theo công thức sau để tạo một khóa riêng lẻ (r) cho tin nhắn:

r = (gk mod p) mod q

Hãy để con số ném vào số của chúng tôi:

r = (93 mod 11) mod 5

r = (729 mod 11) mod 5

Chúng tôi sử dụng máy tính modulo của chúng tôi một lần nữa, nhập 729 và 11, cho chúng ta một kết quả của 3. Vì thế:

r = 3 mod 5

Và sau đó chúng tôi lặp lại thao tác modulo một lần nữa với các giá trị mới để cung cấp cho chúng tôi:

r = 3

Giá trị của chúng tôi cho r được sử dụng làm chìa khóa cho tin nhắn.

Chúng tôi đến với phần khác của chữ ký số, S, với công thức sau:

S = = k-1(H(m) + xr) mod q

Các k-1 không đại diện cho sức mạnh tiêu cực của k, nhưng thay vì tính toán nghịch đảo mô-đun, giống như trong Tìm ra tiểu mục khóa riêng trong phần trước của bài báo chúng tôi đã nói về RSA.

H(m) là giá trị băm cho thông báo mà người gửi đang ký. Thông thường, đây sẽ là một giá trị băm dài được lấy từ thông điệp, giống như trong Hiểu giá trị băm tiểu mục trên, mà chúng tôi đã đề cập khi chúng tôi nói về thuật toán RSA.

Đối với ví dụ này, chúng tôi sẽ giữ mọi thứ đơn giản. Giống như trong phần RSA, chúng tôi sẽ nói rằng thông điệp của chúng tôi, m, Là “Hôm nay trời nóngGiáo dục và đó là hàm băm của tin nhắn H(m), là 10.

Vì vậy, hãy để nhập vào tất cả các giá trị của chúng tôi vào công thức:

S = 3-1 (10 + 2 x 3) (mod 5)

S = 3-1 (10 + 6) (mod 5)

S = 3-1 (16) (mod 5)

Bây giờ, chúng ta có nghịch đảo mô-đun của 3 theo thứ tự 5 (bởi vì 5 là giá trị của chúng tôi cho q), sử dụng cùng một máy tính nghịch đảo mô-đun từ trước đó. Đi vào 3 là số nguyên và 5 là modulo, sẽ cho bạn kết quả của 2. Vì thế:

S = 2 (16) (mod 5)

S = 32 (mod 5)

Hãy để Lùi quay lại máy tính của chúng tôi để hoạt động modulo bình thường, giữ nguyên các tham số mà chúng tôi đã sử dụng trước đó, ngoại trừ:

• Con số một giá trị – 32
• Con số b giá trị – 5

Nếu bạn đã làm điều này một cách chính xác, nó sẽ cung cấp một giá trị cho S của 2. Chữ ký số bao gồm r và S (3 và 2, tương ứng). Người gửi truyền chữ ký số đến người nhận cùng với tin nhắn của họ,Hôm nay trời nóngMùi. Họ cũng sẽ chia sẻ các giá trị của p, q, g và y với người nhận của họ.

Xác minh chữ ký số

Khi người nhận nhận được chữ ký điện tử bên cạnh tin nhắn, họ có thể xác minh tính toàn vẹn và tính xác thực của tin nhắn bằng bộ tính toán sau.

Bước đầu tiên là tìm hàm băm của tin nhắn mà họ nhận được. Người nhận thực hiện điều này bằng cách chạy toàn bộ tin nhắn thông qua hàm băm. Để giữ cho mọi thứ đơn giản và nhất quán, hãy để Lừa nói rằng hàm băm của tin nhắn, H(m) là 10.

Người nhận cũng đã được gửi các giá trị sau mà họ sử dụng trong quy trình xác minh:

• Chữ ký số (r, s) – 3, 2
• p – 1
• q – 5
• g – 9
• y – 4

Tính toán đầu tiên là tìm w:

w = = S-1 mod q

Một lần nữa, S-1 đại diện cho việc nghịch đảo mô-đun. Hãy cùng nhập vào các giá trị của chúng tôi:

w = 2-1 mod 5

Chúng tôi sẽ sử dụng máy tính nghịch đảo mô-đun từ trước đó. Đi vào 2 là số nguyên và 5 là modulo, sẽ cho bạn kết quả của 3 cho w. Bước tiếp theo là tìm bạn1 với công thức sau:

bạn1 = H(m) x w mod q

Hãy để những giá trị của chúng tôi:

bạn1 = 10 x 3 mod 5

bạn1 = 30 mod 5

Quay lại máy tính modulo bình thường, giữ nguyên các tham số mà chúng ta đã sử dụng trước đó, ngoại trừ:

• Con số một giá trị – 30
• Con số b giá trị – 5

Điều này cho chúng ta một kết quả của 0 cho bạn1.

Chúng tôi sử dụng công thức tiếp theo để đưa ra bạn2:

bạn2 = r x w mod q

Hãy để nhập số của chúng tôi:

bạn2 = 3 x 3 mod 5

bạn2 = 9 mod 5

Sau đó chúng tôi quay trở lại máy tính modulo bình thường, sử dụng các tham số tương tự như trước đó, ngoại trừ:

• Con số một giá trị – 9
• Con số b giá trị – 5

Nếu bạn nhập chính xác, nó sẽ cho bạn một kết quả cho bạn2 của 4.

Bây giờ chúng tôi có các giá trị của chúng tôi cho bạn1 và bạn2, chúng ta có thể tìm thấy v, với công thức sau:

v = (gu1yu2 mod p) mod q

Hãy để Lừa ném số của chúng tôi:

v = (90 x 44 mod 11) mod 5

v = (1 x 256 mod 11) mod 5

v = (256 mod 11) mod 5

Chúng tôi quay trở lại máy tính modulo bình thường của chúng tôi, sử dụng các tham số tương tự như trước đó, ngoại trừ:

• Con số một giá trị – 256
• Con số b giá trị – 11

Điều này cho chúng ta một kết quả của 3. Vì thế:

v = 3 mod 5

Sau đó, chúng tôi sử dụng máy tính modulo bình thường một lần cuối cùng, một lần nữa với cùng tham số, ngoại trừ:

• Con số một giá trị – 256
• Con số b giá trị – 11

Điều này cho chúng ta một kết quả cho v của 3.

Nếu tin nhắn là xác thực và đã bị giả mạo, thì v sẽ bằng r:

    v = 3

    r = 3

    3 = 3

Do đó, tin nhắn đã được gửi bởi chủ sở hữu của khóa riêng và tin nhắn đã không bị thay đổi kể từ khi nó được ký.

Ưu điểm DSA & khuyết điểm

Tính bảo mật của DSA phụ thuộc vào việc nó có sử dụng đủ số lượng hay không. Ngoài p, q và g tuân theo các tham số chính xác, giá trị của k cũng cần phải ngẫu nhiên Nó không phải là một giá trị có thể dự đoán được, hoặc một giá trị được sử dụng nhiều lần. Nếu những yêu cầu này không được đáp ứng, thì kẻ tấn công có thể lấy lại chìa khóa.

Mặc dù khả năng này, DSA thường được coi là an toàn miễn là nó được triển khai chính xác và nó sử dụng các giá trị đầy đủ. Mặc dù nó tương đối an toàn, DSA không có xu hướng được triển khai nhiều so với RSA hoặc các phương thức chữ ký số khác. Khi so sánh với RSA, nó có thể tạo khóa nhanh hơn và cũng nhanh hơn trong việc tạo chữ ký số, nhưng chậm hơn trong việc xác minh chúng.

Theo mặc định, phiên bản 7.0 của OpenSSH đã ngừng hỗ trợ các khóa DSA, đây dường như là một dấu hiệu cho thấy thế giới đang di chuyển qua DSA và chuyển sang các thuật toán khác.

ECDSA & EdDSA

RSA và DSA không phải là thuật toán chữ ký số duy nhất, cũng không phải là thuật toán phù hợp nhất cho mọi tình huống. Có một loạt những người khác, chẳng hạn như ECDSA và EdDSA, có tính chất làm cho chúng thích hợp hơn trong những trường hợp nhất định.

Thật không may, chúng dựa vào toán học thậm chí còn phức tạp hơn, chẳng hạn như đường cong elip và mật mã đường cong Edwards. Chúng tôi đã giành được một số chi tiết ngày hôm nay do sự phức tạp thêm này, nhưng chúng tôi sẽ nói về một số mặt tích cực và tiêu cực tiềm năng của họ.

ECDSA

Thuật toán Chữ ký số Elliptic Curve là một biến thể của DSA kết hợp với mật mã đường cong elliptic. Nó cung cấp một mức độ bảo mật tương tự như RSA, nhưng với khóa nhỏ hơn nhiều. Điều này làm cho nó hiệu quả hơn RSA hoặc DSA trong hầu hết các khía cạnh của hiệu suất.

EdDSA

Đây là một thay thế DSA khác, ngoại trừ nó dựa trên các đường cong Twisted Edwards. Nó là tương đối mới khi các thuật toán đi, có cả ưu điểm và nhược điểm của nó. Về mặt tích cực, nó sử dụng các kỹ thuật mới hơn để thêm vào hiệu suất của nó.

Thật không may, các thuật toán mới hơn đã gặp phải sự xem xét kỹ lưỡng, vì vậy nhiều người thận trọng khi quyết định có thực hiện chúng hay không.

Mặc dù vậy, việc sử dụng EdDSA cung cấp hiệu suất cao, chống lại các cuộc tấn công kênh bên, và không cần số ngẫu nhiên duy nhất trong mỗi chữ ký. Ở giai đoạn này, EdDSA có vẻ đầy hứa hẹn và nó đang bắt đầu thấy triển khai rộng hơn, nhưng chúng ta sẽ phải chờ xem liệu các nghiên cứu trong tương lai có tìm thấy lỗ hổng bảo mật nào không.

Chứng thư số

Bất cứ ai cũng có thể dễ dàng tạo ra một cặp chìa khóa, thậm chí là một kẻ tấn công. Vì vậy, những gì ngăn ai đó tạo ra một loạt các chìa khóa và giả vờ rằng họ là Tổng thống, hoặc đặt ra như bất kỳ ai khác?

Chà, không có gì ngăn ai đó tuyên bố rằng họ là một người khác, nhưng có một hệ thống cho phép người khác xác định xem người đó có thực sự là người họ tuyên bố hay không. Nó gọi là cơ sở hạ tầng khóa công khai (PKI), và nó liên quan đến chứng chỉ kỹ thuật số liên kết khóa công khai cá nhân hoặc thực thể với danh tính thật của họ. Những chứng chỉ này được ký bởi những người khác để chỉ ra mức độ đáng tin cậy của chứng chỉ.

Bạn có thể so sánh quy trình với việc sử dụng công chứng viên để xác minh tài liệu. Nếu ai đó có một bản sao giấy khai sinh, bạn có thể hoài nghi về việc nó có hợp pháp hay không. Nếu cùng một giấy khai sinh được ký tên và đóng dấu bởi một công chứng viên, bạn sẽ có nhiều khả năng tin rằng đó là một bản sao thực sự.

Tại sao?

Bởi vì chữ ký và tem cho thấy một thực thể công cộng đáng tin cậy đã nhìn thấy cá nhân và giấy khai sinh gốc của họ, sau đó xác minh rằng bản sao trên thực tế là hợp pháp. Công chứng viên xác nhận bản sao giấy khai sinh và đặt uy tín của họ đằng sau nó với chữ ký và dấu của họ.

Sự tin tưởng mà chúng tôi dành cho công chứng viên được chuyển sang bản sao giấy khai sinh, cho phép chúng tôi tin tưởng nó nhiều hơn một người chưa được công chứng.

Có hai loại chứng nhận chính, cchính quyền (CA) và trang web tin cậy.

Cơ quan cấp chứng chỉ

Cơ quan cấp chứng chỉ các tổ chức đáng tin cậy chạy kiểm tra các cá nhân hoặc tổ chức để xác minh xem họ có phải là chủ sở hữu hợp pháp của khóa công khai không. Nếu séc tiết lộ rằng cá nhân là chủ sở hữu thực sự, thì cơ quan cấp chứng chỉ sẽ ký chứng nhận bằng khóa riêng của họ, biểu thị rằng họ đã hoàn thành séc và tin rằng khóa cá nhân và khóa chung được liên kết hợp pháp.

Miễn là chúng tôi tin tưởng cơ quan cấp chứng chỉ và quy trình xác minh khóa của họ, thì chúng tôi có thể tin tưởng vào chứng chỉ đã được ký bởi họ, và do đó, khóa công khai thực sự đại diện cho cá nhân đó.

Tùy thuộc vào loại chứng chỉ và ứng dụng của nó, các cấp khác nhau có thể có các quy trình xác minh khác nhau và do đó thể hiện mức độ tin cậy cao hơn hoặc thấp hơn.

Trang web của niềm tin

Mạng tin cậy hoạt động theo một tiền đề tương tự, ngoại trừ tở đây không có cơ quan trung ương như cơ quan cấp chứng chỉ thực hiện quy trình xác minh và ký giấy chứng nhận.

Thay vào đó, trang web của niềm tin dựa vào các cá nhân khác để ký chứng chỉ, đặt danh tiếng của họ vào liên kết giữa cá nhân và khóa chung. Hệ thống này chủ yếu được sử dụng với PGP, nơi người dùng có thể dễ dàng tạo chứng chỉ của riêng mình.

Nó hoạt động như thế này:

Hãy nói rằng bạn có hai người bạn muốn chứng nhận của họ được ký để chứng minh rằng họ là chủ sở hữu hợp pháp của các khóa công khai tương ứng. Bạn biết rõ những người này và họ cho bạn xem ID chính phủ của họ, điều này khiến bạn hoàn toàn chắc chắn rằng họ là chính họ, và do đó họ là chủ sở hữu thực sự của các khóa công khai mà họ đang yêu cầu.

Vì bạn biết rằng họ là chủ sở hữu hợp pháp của khóa công khai của họ, bạn rất vui khi sử dụng khóa riêng của bạn để ký chứng chỉ của họ, đánh cắp danh tiếng của bạn và nói về cơ bản, họ đã xác minh danh tính của những cá nhân này và họ là ai họ tự xưng là người Ý. Hai người bạn này sau đó có thể làm điều tương tự với bạn.

Hãy nói rằng mỗi người trong hai người bạn của bạn có hai người bạn khác muốn có chứng chỉ của họ. Nếu hai người bạn của bạn ký các chứng chỉ khác này, thì bạn có thể sử dụng niềm tin mà bạn có trong bạn bè của mình để chấp nhận rằng những người khác này thực sự là người mà họ nói họ cũng như vậy.

Sau đó, bạn bè của bạn bè của bạn có thể ký giấy chứng nhận của những người mà họ tin tưởng và cuối cùng, cuối cùng xây dựng một mạng lưới lớn các cá nhân đáng tin cậy. Khi các web này đủ lớn và được kết nối với các web khác, chúng có thể được sử dụng như một phương tiện để tin tưởng bất kỳ ai khác trong mạng.

Càng nhiều chữ ký trên một chứng chỉ, đặc biệt nếu chúng là chữ ký của các cá nhân rất đáng tin cậy, bạn càng có thể tin tưởng vào chứng chỉ kỹ thuật số của ai đó và liên kết giữa khóa chung và danh tính của họ.

Người dùng PGP thường tổ chức các buổi ký kết quan trọng nơi mọi người tụ tập để kiểm tra danh tính và chứng chỉ kỹ thuật số của họ được ký. Những cuộc tụ họp này giúp đưa những người mới vào mạng.

Mặc dù đi kèm với một số phức tạp, lợi thế của hệ thống ủy thác là không có cơ quan trung tâm nào có thể bị hỏng.

Chữ ký số có an toàn không?

Trong một ý nghĩa chung, chữ ký số được bảo mật trừ khi khóa riêng của người đăng ký đã bị xâm phạm. Nếu chủ sở hữu đã thông báo cho người khác, để lại khóa riêng được viết hoặc bị đánh cắp theo cách khác, thì kẻ tấn công có thể ký điện tử tin nhắn như thể họ là chủ sở hữu.

Điều này có thể dẫn đến kẻ tấn công mạo danh nạn nhân của họ hoặc giả mạo dữ liệu của họ. Đây là một vấn đề bảo mật rất lớn và bất kỳ ai nghi ngờ rằng khóa của họ đã bị xâm phạm đều phải thu hồi chứng chỉ kỹ thuật số đã liên kết chúng với khóa chung của họ và được cấp mới.

Có một vài cảnh báo khác khi nói đến tính bảo mật của chữ ký số. Một thuật toán chữ ký số thích hợp nên được sử dụng, và nó cũng cần được thực hiện đúng. Bên cạnh đó, cũng cần có cách liên kết khóa công khai với chủ sở hữu của nó, thường là thông qua các chứng chỉ kỹ thuật số.

Miễn là các yêu cầu này được đáp ứng, bạn đang tuân theo các thực tiễn tốt nhất trong ngành và khóa riêng của bạn chưa bị xâm phạm, sau đó chữ ký số là một cách tuyệt vời để cung cấp tính xác thực, tính toàn vẹn và không thoái thác dữ liệu.

Dữ liệu có cấu trúc bởi Kai Stachowiak được cấp phép theo Muff